1The language of mathematics
The introduction of on November 30, 2022 took the world by storm. The use of generative AI or large language models is encouraged throughout this course. It is my hope that you will learn mathematics on a deeper level by communicating with the machine using careful prompt engineering. Good prompts seem to resemble clearly written text.First we need to introduce some formal notation to be able to talk clearly about mathematics and also in a reasonable way formulate mathematical models of the real world. In modern mathematics the concept of a set is crucial. It is a bit tricky to define this precisely. We will go on and define the basic concepts of what is called naive set theory.1.1 Black box warnings
Modern mathematics is perhaps not like anything you have encountered so far. It calls for a lot of focus and precision, especially when writing down solutions to problems. It is a bit like programming a computer. There is no room for imprecision and half-baked sentences.This course amounts to ECTS or approximately hours. Suppose that you spend a week studying for the exam, say hours. Lectures, exercise classes and MatLab amount to hours hours. This leaves around hours for your own study and immersion. Put in other terms, you are supposed to work around hours per week outside classes for this course. With classes, each week calls for hours of work. There is a very close relationship between the amount of hours you log each week and your result at the exam. To state the obvious: numbers don't lie. If you put in the time, you will almost certainly do well. Try to allocate time for IMO in your weekly schedule and please (ab)use all the help that is provided.Also, computers are exceptionally fun, but be careful! Nothing really beats a clear thinking human mind. To wit, I asked WolframAlpha to solve a certain optimization problem and it came up with the answer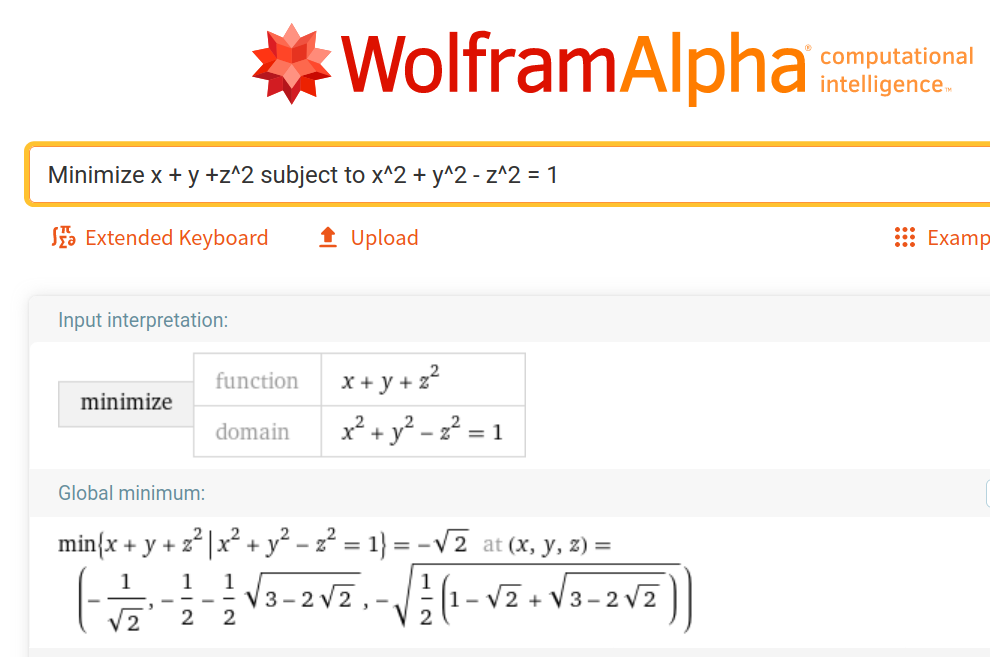
1.2 Computer algebra
We will use the computer algebra system Sage in exploring and experimenting with mathematics. This means that you will have to write small commands and code snippets. Sage is built on top of the very wide spread language python and you can in fact enter Python codeOne may also enter code in several other languages in the Sage input windows in this text. Below is an example of a basic graphics command in Sage. Push the Compute button to evaluate.You can install Sage on your own computer following the instructions on https://www.sagemath.org/.
Did you notice that you can edit and enter new commands in the Sage window?
Do the following problems using Sage based on the Sage guided tour.
- Consider . Plot the graph of from to . Computing does not make sense. Do you see a way of assigning a natural value to using the graph?
- Find an approximate solution with four decimals to the equation . This is an example of an equation, that can only be solved numerically. Try first plotting the graph of from to . Then use a suitable function from the Sage guide.
- Compute with decimals.
Compute the sum
without using a computer.PS: If you have a subscription with WolframAlpha PRO, you can unlock the Step-by-step solution to get the answer to this (and the bonus question below). Try to do it yourself! Nothing beats the warm feeling of coming up with a killer idea after struggling for some time.Bonus question
Generalize your answer/method to computing the sum
for .
1.3 Objects or elements and the symbols and
Mathematics can be broadly viewed as handling objects precisely according to a specific system of rules. The first element of precision is in distinguishing the objects and deciding when they are the same. This calls for notation. If two objects and are the same, we write . If they are different we write .You may laugh here, but identifying objects is really one of the fundamental tasks of mathematics. It is not always that easy. Even though objects appear different they are the same as in, for example The first example above is an identity of fractions (rational numbers). The second is an identity, which calls for knowledge of the sine function and real numbers. Each of these identities calls for some rather advanced mathematics. Use the Sage window above to reason
about equality in the quiz below. In each case describe the objects i.e.,
are they numbers, symbols, etc.? Also, please check your computations
by hand with the old fashioned paper and pencil, especially .
Click on the right equalities below.
You know that . Use Sage to find a similar identity
for .
Go back and look at (the beginning of) Exercise 1.4.
1.4 Sets
A set is (informally) a collection of distinct objects or elements. A set is an object as described in section 1.3 and it makes sense to ask when two sets are equal.
Two sets and are equal i.e., if they contain the same elements.
Give a precise reason as to why the two sets and are not equal.
Is it possible for a set with elements to be equal to a set with elements?
Sets may be explored using (only) python. This is illustrated in the snippet below.
Come up with three lines of Sage code that verifies . Try it out.
1.4.1 The empty set
There is a unique set containing no or zero elements. This set is called the empty set and is denoted i.e., Not surprisingly the empty set is reflected as the empty list in Sage. The empty list has zero elements.
For some reason (perhaps a good one) python does not accept as input for the empty set.
Why is this? Evaluate the python snippet below and explain.
1.4.2 Sets of numbers
A set could also be the natural numbers (yes, I want as a natural number: is very natural, although it came late historically) or the set of integers These sets are called infinite, since they contain infinitely many elements. Even though the natural numbers seem as easy as one, two three, they contain wonderful and deep mathematical mysteries, such as the nature and distribution of the prime numbers . Also please respect, that the negative numbers like have caused confusion for centuries.We also have the set of rational numbers (fractions) and the set of real numbers. The real numbers contains all the possible numbers that we encounter in this course.We will not define the arithmetic operations (like addition and multiplication) on and formally. I will assume that you know how to add and multiply fractions, and that you do not make mistakes like Similarly, I will assume that you know that a rational number stays the same, when the numerator and denominator is multiplied by the same non-zero integer. For example, In fact, The computation above says that it is straightforward to add pizza slices of the same size (one sixth), but that you need to think a bit when adding one half pizza slice and two pizza slices of size one third.
Click on the right equalities below. Do not use Sage (or any computer)!
1.4.3 Notation and rules for arithmetic operations
Please do not use the symbol for multiplication coming from your favorite computer algebra system. Nothing is worse than looking at notation like in a written assignment. In the language of mathematics (1.1) is written When using variables multiplication is simply an elegant small space and is used with numbers. Also recall the important distributive law for handling expressions formally. It says that Notice that you can read the distributive law from right to left i.e., you may write instead of .
Verify that (1.3) is true for some specific non-zero numbers. Also
convince yourself that WolframAlpha actually
accepts space (between numbers and variables) as multiplication.
Suppose that and . It seems
that computing involves two multiplications and one addition. Multiplications are
expensive operations on a computer. Is there a way of computing
with only one multiplication and one addition?
1.4.4 The symbols and
The symbol is ubiquitous in set theory (and mathematics). It means belongs to or is an element of as in , where is an element and is a set. The symbol means is not an element of as in meaning is not an element of .
, but . This exercise actually has possible correct solutions
if is in the second empty box and in the fourth empty box.
1.4.5 Subsets and the symbols and
If and are sets, then At times, the symbol is used instead of . In our context these two symbols mean the same. However, the notation means that and . For example, and . means that every element of is also an element of . In this case we say that is a subset of . We also use the notation to indicate that and . In this case we say that is a strict subset of . MentimeterWe have for example that What does mean? Here we have to be a little careful. We want this notation to mean that is not a subset of . In order for to be false, there must exist , such that . This is the meaning of . For example, since and .
The set is not a subset of , simply because does not belong to .
This exercise actually has possible correct solutions.
List all the subsets of a set with five elements. In general, how many subsets does a set with elements have?
The empty set has elements. A set with elements has subsets. In general a set with
elements has subsets.
1.4.6 Intersections, unions and the symbols and
Suppose that we have two sets and . Then the intersection is the set consisting of the elements in both and . This is illustrated in the socalled Venn diagram below.
Let , and . Verify by hand (no computer) that
- .
- .
- .
- .
Given two sets and , is it true that
and ?What about ?Suppose that and are two finite sets. Is it true that
What about
Seriously, both formulas are wrong. Can you come up with the correct
version of the formula for ?Use your correct formula to find a formula for
viewing as the first set and as the second set. Here you need
the formula
Why is this formula true? Finally, explain why
Hint
If you are attacking the last part of this exercise using Exercise 1.43, you
may find it useful to notice that two sets are equal i.e,
if and only if
Also,
There is one more operation called the symmetric difference between two sets and . It is
denoted . Experiment in the python window below to find out exactly what it does.
Is it true that ?
The following is an excerpt from the infamous Beredskabsprøve Datalogi.
Let and denote sets. Which of the following are true?
For some sets and we can have
1.4.7 Pairs, triples and tuples
Given two sets and we can form the new set , which is the set of pairs , where and . For example, The set is also called the Cartesian product of and .Mentimeter
Consider two pairs and . What is a natural way of defining
equality between these pairs i.e., ?
The Cartesian product can be computed in python as shown below.There is no need to restrict ourselves to pairs. We might as well
consider triples i.e.,
the set of all , where , and are sets, or
for that matter general tuples
of any length , where . Based on the above example with tuples we have,
You may check this using the python snippet below.
For a given set and we define the -fold cartesian product of as
Have you seen before? Perhaps plotting points or graphs? In the same way, is there a geometric
way of thinking of ? Does exist in the real world?
Let and be two sets. Is ?Let be any set. What is ?Let and be four sets. Is
Is
See Exercise 1.25.
Use python to solve Exercise 1.24 by playing with (and extending) the code below.
1.5 Ordering numbers
Let us be a little rigorous and introduce the (usual) ordering on our numbers with addition and multiplication using almost full blown mathematical formalities. First the formal definition for two integers :Notice that implies that (and ).
Along this line we also define if and .
Assume that and that . Then drag and drop the
elements from the left to the right below to explain that
.
By assumption .
This means that
This means that
To show that , we need to show that
.
But . Therefore,
But . Therefore,
, since
Suppose thatAs an example, this could be assuming and and then
arguing that .
for three integers . Argue
from the definition in (1.4) that by using the definitions of
and to conclude that .
Suppose that and , where . Conclude that
What if we only assume that ? You are welcome to experiment with
some concrete numbers like and . In the end
you should be able to come up with an argument using the variables
with the given assumptions.
You can
see that this definition agrees with our preconception that
To be precise, writing is nonsense, since is only defined for two integers in (1.4).
How is one supposed to interpret for example? Go ahead and formulate (1.5) correctly comparing only two integers at a time.
How does Python/Sage interpret ? Find out using the Sage snippet below.What about ? What about ?
We wish to compare the two rational numbers and deciding
precisely how they are ordered:
How does one come up with the definition in (1.6)? Why not
instead of ? The reason is that
we want the order on to be related to the one we already defined on
the subset . It should respect multiplication by positive numbers just
as in Exercise 1.28. If we want this to hold, we are forced
to the definition in (1.6), since
Order the arguments below so that they constitute a coherent explanation of the
statement that if
then
By definition this means that .
We are assuming that .
For integers we know that the rule
holds. Therefore
we need to show that .
Since and is a consequence of , we are
done if we know this is true.
However, this is a consequence of our assumption .
To show that
we need to argue that .
we need to show that .
Similarly to the quiz above, assume that
Write down a precise argument showing that
You may seek inspiration in Video 1.51 for
how to mix math and words (even though
it is further ahead).
On Twitter, Raman Gupta posted the note below For a natural number ,
For example, and . What is the answer for the
question in the note?
For a natural number ,
For example, and . What is the answer for the
question in the note?
The exercise below shows that our trick for finding rational numbers
in between two given rational numbers can be made into a machine for
generating all positive rational numbers!
Experiment a bit with Sage: define a function , which computes
Then look at
Can you spot the system in the fractions in the diagram below?
 Once you see the system, extend the diagram with the next level downwards. Is every
positive fraction present in this diagram if one keeps adding levels?
Once you see the system, extend the diagram with the next level downwards. Is every
positive fraction present in this diagram if one keeps adding levels?
Suppose that
and . Then for
we have and . If is
a positive fraction, such that
show that
1.5.1 Subsets of numbers and first elements
In a set equipped with an order, it is intuitively clear what a first element should be. For example, the natural numbers has as its first element. On the other hand the set of integers does not have a first element (it is "infinite to the left").In fact every non-empty subset has a first element. This follows from a rather special property of : there can be only finitely many natural numbers smaller than a given one. This is not true for . Here there are infinitely many integers smaller than any integer.
If is a set with an order and is a subset, then formally is a
first element of if for every element .
Mentimeter
Give an example of a subset of that does not have a first element. Does the
subset of even numbers have a first element? Does the empty subset have a first element?
Can a non-empty subset of a set with an order have two different first elements? I need to
be precise here. I am assuming that the order (naturally) satisfies: if
and are two elements from the subset and and both hold,
then .Do the orders we defined on and satisfy the above property?
If , where , then . If , then .
But
In other words, is an integer that satisfies and .
What integer is ?
Consider the subset of consisting of positive fractions i.e., rational numbers .
Does this subset have a first element?
1.6 Propositional logic
We have seen quite a few mathematical statements that ended up being true or false. Such statements are called propositions. Here are two examples of propositions usings sets (in python):
What exactly are the two propositions in the above python window written
up in mathematical terminology? Notice that the symbol == is
a programming construct. It is not used in mathematics notation.
Propositions can be combined into
new (compound) propositions. Take for example the propositionsThen ( and ) is a perfectly good
new proposition reading it rains and it is cloudy. The same goes for (if then ), which reads
if it rains then it is cloudy. The proposition (if then ) reads if it is cloudy then
it rains. This proposition is (clearly) false.
We need some notation to describe these compound propositions:
The compound propositions are either true() or false () depending on
and . The dependencies are displayed in the truth tables below.The tables for the compound propositions and also
are not too hard to grasp. The table for
raises a few more questions. Why is true?
I will not go into this, but just point out that there are
many explanations available online and,
perhaps more importantly, refer you to Exercise 1.40 and the remark below.
Here is a statement about real numbers
This statement reads: no matter which real number you pick, if ,
then . We definitely want this to be true. Being true means
that (1.7) must hold for all numbers , also ,
which reads
The above statement is an example of a false implies true statement, which
we want to be true: even though is negative, its square is positive.In general terms, in proving the statement that holds for every in
some set , we are really only interested in for which is true, since
is our assumption. We still need to be true for for
which is false. This is assured by the truth table for , since
and are both true.
Suppose that we are presented with four cards
with a (natural) number on the front and the color
blue or red on the back.
In (1.8), the first and third cards are shown with their fronts facing up and
the second and fourth cards are shown with their backs facing up.A claim (proposition) is made that if a card has an even number on the front, then it
must have the color blue on the back.Your task is to verify this for the cards above. Of course you can
do this by turning all four cards, but is there a way of checking this
by turning less than four cards?What if we add the claim, that if a card has the color
blue on the back, then
it must have an even number on the front?
Find two propositions and so that the claim reads
.
Explain why Python/Sage thinks that the valueThanks to Gerth Brodal for pointing this out to me of
is False! Notice that you are dividing one by zero in the last "integer" above.
In the exercise below you will see for example that
is the same as .
Two propositions are considered the same () if they have the same truth table. Verify, by
filling out and comparing truth tables, that
Can you use the setup up in Exercise 1.42 to verify that
for three propositions and ? Verify an analogous identity for
The notation is used frequently. It means that both
and are true i.e.,
Mentimeter1.6.1 The symbols and propositions with variables (predicates)
In mathematics one usually reasons with propositions with variables, such as . A proposition with variables is usually called a predicate.In order to evaluate a predicate with a variable , one must first specify to which set the variable belongs. For example, the predicate given by does not make sense if is taken from the set of letters in the English alphabet (not unless you give an interpretation of , and in this set). However, if , then certainly makes sense. Whether is true depends on .For example, is false, whereas is true. This leads us to the existential and universal quantifiers and . The former reads there exists and the latter for every.For example, the predicate is true and so is The symbol ":" above means "such that"Therefore reads "there exists in , such that is true".. Also, is false, because is true. Linking ":" with one may say that
for a general predicate . This statement can only be false if there exists ,
such that is false (see the truth table for above). In particular, is a true statement!In general,
So we do not really need the quantifier , when we have
and , but is convenient and used all
the time. Notice that is a false statement!The quantifiers are important to learn and apply when expressing
mathematical ideas. So is the use of predicates
in writing up subsets: if is a set, a variable taking values
in and a predicate (making sense in ), then
For example, if , then
Suppose that are predicates with a variable taking values
in , then we often use the notation (using instead of )
It also makes sense to have predicates with more than one variable. With
variables in , such a proposition could be
Consider the predicate from Remark 1.44. Write
down the elements in
Is
an infinite set?
Explore the fascinating world of prime numbers and learn about twin primes.
List the elements in the following subsets.
You have previously encountered systems of linear equations like
The solutions to (1.9) can be identified with a subset of
. Define this subset precisely i.e., write the subset as
where is a predicate in the variables .
Suppose that and
Then write down precisely what is i.e., find suitable predicates in the
variable , such that
and
Consider the subset of pictured in the drawing below Express as
where are predicates in the variables .Hint
Express as
where are predicates in the variables .Hint
The following is yet another excerpt from the infamous Beredskabsprøve Datalogi.
A predicate in the variables could be something like
Express as
where
and and are suitable predicates in the variables .
Which of the following are true?
1.6.2 The use of implication () and bi-implication ()
Usually and are applied to link propositions in a logical argument. An example is for integers . To be completely precise, I should here write but one often writes with words as for example for integers .To be one hundred percent precise (1.10) means formally, that Here is true and similarly (by using the definition (see (1.4)) of in ). So the use of is valid. A somewhat simpler example is However, for we cannot link the two propositions by , simply because is false (for ).1.7 What is a mathematical proof?
Most professional mathematicians rarely think about the precise definition of a proof. During many years of training they have assimilated knowledge by experience. Therefore many proofs seem born out of witchcraft containing several magical devices.However, many proofs appearing in respected mathematical journals, submitted by respected mathematicians, have turned out to contain errors. Recent developments in automated proof systems like Coq and LEAN show promise in checking proofs like for example the famous four color theorem.Informally a proof of a proposition , consists in arguing that an implication is true by first assuming . Usually this is done not only through one implication , but through a series of intermediate implications where the last proposition is . If is true, this will constitute a proof that is true. Just like in (1.5), there is an imprecision here. Can you tell what it is?In this section we will illustrate a simple mathematical proof of the proposition: where i.e., the square of an odd natural number has to be odd. This seems true for a first selection of examples: .First we need to know what means. What does it mean exactly for a number to be odd? This means that it is not divisible by or that there exists another natural number , such that . So Therefore we need to show that Notice that I had to change into in the second proposition above. The two variables are not the same: is associated with and is associated with .Let us assume that . Now we need to argue that for some . You stare at this for a while and notice that we should use the assumption in computing : Thus, using our assumption we may conclude that if , then where . This completes the proof.The beauty here is that we have verified for all odd natural numbers that their square is odd. Not just a finite selection like .Below I have given a very detailed walk through of the proof above. It exemplifies how to write up the proof mixing words and mathematics. In many ways a proof is like a detailed argument in a court case, except that the rules of mathematics are universal. You need the absolute truth.1.7.1 Proof by contradiction
A proposition is either true or false. This seemingly obvious statement goes by the name of the law of excluded middle and dates back to the writings of Aristotle.
An irrational number is a (real) number that is not rational. It is a
startling fact that such numbers exist, but they do! The square root of two
is an example.
We will prove that there exists two irrational numbers , such that
is rational.Consider the proposition given
by
Either is true or false. If is true we are done putting . If not, then
must be false and is irrational. But then
and we are done putting and .
We know that is multiplied by itself, but can you define in a similar
precise way?
Here you need help from the special functions and .
So which one is it? Is
rational or irrational?
The law of excluded middle can be turned
into a powerful proof technique called proof by contradiction.Suppose we wish to establish that is true. Then we turn things upside down by
assuming that is false i.e., that is true. If we then
by logical deduction can show that
for some proposition , which is demonstrably false, then cannot be true (since
true false is false). Therefore
must be false and must be true by the law of the excluded middle. This technique is used all the time!Perhaps the two most famous proofs by contradiction in all of mathematics are due to Euclid. The first one is about the infinitude of the prime
numbers.
Here one assumes to begin with that
there are finitely many prime numbers and follows this through to a contradiction.
See Exercise 1.56.MentimeterThe second
one (perhaps even attributable to Artistotle) is about the irrationality of . Here one assumes to begin with
that is rational and follows this through reaching a contradiction. See
Exercise 1.57.
This is advanced mathematics! Try to make sense of the famous
Gelfond-Schneider theorem.
We will give an example of a proof by contradiction using a previous exercise: let
be the proposition that
the subset
of
does not have a first element. Recall the definition of a first element in
the context of : is a first element if
So if is a first element in , there cannot exist , such that
.The proof by contradiction in this case, runs as follows. Assume i.e., that
has a first element say
Then using we can form
and you can checkCheck that . that and i.e., is not a first
element. So our assumption that has a first element immediately leads
to the conclusion that does not have a first element. In fact, we have proved
Therefore (the wrong assumption)
has to be false and thus must be true.
Consider the first prime numbers
Check that
are prime numbers by using the Sage window below (factor gives
the prime factorization of a natural number).Is it true in general that
is a prime number?Assume that we know that every natural number must be divisible by a prime number. Show how the
assumption that there are only finitely many prime numbers say
leads to a contradiction by using that the natural number
must be divisible by a prime number.
Suppose that . Prove that
Suppose that
Show that this implies and that and are even numbers.Given the above, write up a precise proof that
using proof by contradiction.You may wonder what is so special about rational numbers. Which property does
break? You can explore this by looking at the decimal expansion of
some fractions below.However, is an algebraic number being a root in the
polynomial . In general an algebraic number is a number,
which is a root in a polynomial with coefficients in .
1.7.2 Proof by induction
A precocious GaussSee the article Gauss's Day of Reckoning for some history of this anecdote. proved the formula at the age of seven displaying remarkable ingenuity for his age. Lesser mortals usually use induction to prove this formula. Gauss was asked along with his classmates to compute the sum of all natural numbers . Using his formula he quickly came up with the correct answer . His classmates had to work for the entire lesson. Suppose that the formula in (1.11) is viewed as a proposition . To prove the formula we need to prove it for all natural numbers (you can easily see that and are true) i.e., we need to prove An induction proof is a way of proving this statement by showing two things:
Suppose that are infinitely many propositions given by . Then
is true if
- is true.
- is true.
Suppose by contradiction that there exists , such that
is false. Then the subset
is non-empty. Therefore it has a first element .
Here , since is assumed to be true. So we
know that is true and that
is true. But the latter
implication is a contradiction, since true implies
false is false.
What happens if is replaced by and by in Theorem 1.58?
Let us see how an induction proof plays out in the above example
with the statement that
Clearly is true. We need to prove , so
we assume that holds i.e., that (1.12) is true.
Then we may add to both sides of (1.12) to get
Here the right hand side can be rewritten as
which is exactly what we want. This is the conjectured formula for
the sum of the numbers . Therefore
we have proved that and the induction
proof is complete.Mentimeter
For a real number , the extremely useful formula
holds. Let us prove this formula by induction. For this amounts to the identity
which is true since . We let denote
the identity in (1.13). We have seen that is true. The induction step
consists in proving . We can prove this
by adding to the right hand side in (1.13):
Real life application
In order to pay for a house you borrow DKK at an interest of
per year. You want to pay off your debt over years by
paying a fixed amount each year. How much is the fixed yearly
amount you need to pay?Let us analyze the setup: suppose that the fixed yearly amount
is . We will find an equation giving us in terms of
and . Put .After one year you owe
After two years you owe
After three years you owe
In general after years you owe
Since we want to be debt free after years, the yearly payment will have to satisfy
By the formula (1.13), we get
Here can be isolated giving the formula
With the current (August 2023) interest rate around five percent, you pay a fixed monthly
amount of around 5420 DKK (up from 3200 DKK in 2021, when the interest rate was one percent) for borrowing one million DKK over years.
Verify the computation (induction step) in (1.14) i.e., explain
the operations used to go from the left to the right of the two equalities.
Locate the mistake in the following fake induction proof of the curious fact that
for every .Let be
the proposition . Then is true.We wish to prove that assuming that are true:
This shows that and therefore that for every
.
Prove by induction that the sum of the first odd numbers is
given by the formula
i.e., for we have
Prove by induction that
,
Prove using the idea of induction that
for .
The last exercise related to induction concerns the famous pigeonhole principle. The statement itself looks innocent, well almost ridiculous, but it is very powerful. Even the go-to website
mathoverflow for research mathematicians has
a quite nice thread
about this.
Prove the following by induction on : if items are put into containers and
, then at least one container must contain more than one item.
1.8 The concept of a function
A function is a crucial concept in mathematics. In Sage (actually python here) a simple function can be programmed likeThe code above seems to take a number and returns the number plus one. This (f) is in fact a function taking as input a number and returning as output the number plus one. Notice that we do not even know which numbers we are talking about here. In mathematics we need to have a more precise notion of a function. Mathematically a function takes values from a set and returns values in a set . In details, it is denoted and the value associated with is denoted .The above python function could more formally be denoted as with if we are dealing with the integers, but we cannot tell from the code.Well, to be fair ...
To be completely fair, it is possible from Python 3.5 to add type annotations to functions, so that we could write
If you want the super precise mathematical definition of a function, I
will give it here. A function is a subset
, such that
. In words it states that a
function is a subset of , containing pairs
having only one second coordinate for every first coordinate.The everyday working definition of a
function is more intuitive: a machine taking input from some set
and giving output in some set . The uniqueness of the output
is encoded in the mathematical definition of a function.def f(n: int) -> int: return(n+1)
Please notice that a function is a very, very general concept. It is not just something
that you draw as a graph on a piece of paper. Of course, you can draw a function
like :
 Generally, a function is given by a machine, formula or algorithm that
computes for every . Nothing more, nothing less. It really has nothing to
do with a graph (even though graphs can sometimes be useful for visualizing certain functions like ).
Generally, a function is given by a machine, formula or algorithm that
computes for every . Nothing more, nothing less. It really has nothing to
do with a graph (even though graphs can sometimes be useful for visualizing certain functions like ).

Good examples of functions can be found in the cryptographic hash functions. They are examples of complicated functions , where
is infinite and finite. Here could be data like plain text files and could be
a bit number. This is the setup for the widely used sha-256 cryptographic hash function.
The whole point of a cryptographic hash function is that it must be humanly impossible to
compute with given A pair with is called a collision.
In fact, sha-256 is used in the Bitcoin block chain. The precise definition of
sha-256 can be found in FIPS PUB 180-4 approved by the Secretary of Commerce.Other interesting functions output a bounded size digital footprint (checksum) of a file (like md5). This is very useful
for checking data integrity of downloads over the internet. The md5 hash is a bit number.Instead of listing or bits for the hash value one uses hexadecimal notation with digits
in 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , a, b, c, d, e, f. A pair of hexadecimal digits then represents
a byte or bits. Output from sha-256 and md5 consist of and hexadecimal
digits respectively. You are welcome to experiment with these two hash functions in the
Sage window below.Another hashing function is NeuralHash (see also GitHub) constructed using deep learning. It is used in Apple's Child
Sexual Abuse Material (CSAM) technology.
Mentimeter
What is the sha-256 hash of your name? Change a
few letters and recompute. Do you see any system? What about the md5 hash function?
Can you find two different strings with the same md5 hash using your computer?
I have not answered the last question myself, but I am told that it is possible to find
a collision for md5 using a garden variety home computer. Browsing the internet, it
seems that the two strings and given in hexadecimal notationThis notation represents a sequence of bytes given by pairs of hexadecimal digits by
d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f89
55ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5b
d8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70
d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f89
55ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5b
d8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70
1.8.1 Notations for defining a function
If is a function and is a finite set, then you can define using a simple table. This is best illustrated using an example. Suppose that and Then is expressed in table form as Very often the bracket (or Tuborg in Danish) notation is used. It is similar to if-then-else statements in programming: defines the function that outputs if the input and if . In python we may express this as
What is and for the function defined in (1.15). Draw
the graph of . Come up with a function , where it
does not make sense to draw a graph.
We now define three very important notions related to functions.
Let be a function. Then is called
- injective, if for every .
- surjective, if for every , there exists , such that .
- bijective, if it is both injective and surjective.
Is a cryptographic hash-function as defined in Example 1.68 injective?
Suppose that
We define a function by the table
Is injective? Is it surjective? Is it possible to adjust the table so that
becomes injective?
Is it possible to adjust the table so that
becomes surjective?
Consider the function given by
where .
Is injective? Is surjective? Suggest how to change and so that becomes
bijective.
Consider the function given by
Show that is bijective.
Write down precisely how the truth table for may
be expressed in terms of a function . What are the sets and in this case?
1.8.2 Composition of functions
Given two functions and , where , we define a new function by This notion calls for some reflection. We have a total of four sets in this definition: and and, not to forget, the condition that . If this last condition was not satisfied it would be meaningless to apply the function to . I hope the diagram below helps the understanding.
The concept of a function is powerful and underlies functional programming in computer science: every computation can be realized as applying a composition of functions to an argument. This is exemplified in the computer language
Haskell.
Suppose that
and that and are given by the tables
Compute the table for . Show that is not
injective. Adjust the table for so that becomes bijective.
Consider and given by
What is as a function from to in terms of ?
1.8.3 The inverse function
If is bijective, then we may define a function , so that for every and for every . This function is denoted .How do we define for ? Well, since is surjective, we may find so that . Now, we simply define We cannot have in with , since is injective. We only have one choice for in (1.16). Therefore (1.16) really is a good and sound definition.
Let , where be given by
Compute .What if the definition of is changed to
Does make sense here?
What is the inverse function of given by ?
What is the inverse function of , where and
?
1.8.4 Neural networks
Having defined functions and composition of functions, we can deflate the term (deep) neural network, which is often clouded in magic and mystery.A neural network is a special case of a function where and . Neural networks are often compositions of many intermediate functions called (hidden) layers.
A function such as (1.17) can
be written
where are functions .
In a neural
network the functions are viewed as neuronsTo be precise, the functions should be viewed as synapses. Depending on their
input they either fire or do not fire a signal. Classically this is
modelled by the perceptron,
which is a function of the form
for fixed numbers (called weights) and a number (called the threshold).
If the weighted sum is above the threshold, the neuron
fires (returns the value ). If not it does not fire (returns the value ).
Consider the three perceptrons , where
and
Let . Then is
a composite function of two functions
and . Write down these functions.Hint (Illustration courtesy of William Heyman Krill).
(Illustration courtesy of William Heyman Krill).
Have a closer look at (1.18) in order to understand how
functions from to are expressed. Notice that
our notation is a bit inconsistent when it comes to types. For example,
the function should really be
denoted instead of , since it takes input from
. This is remedied in the (hopefully easy to understand) python code below.
Compute
and .Relate the perceptrons and to the illustration
below. What do you think the red and blue line illustrate? What does
it mean that a dot is solid compared to hollow? What is special
about points between the red and blue lines? Try to relate and to the illustration.
Give weights and a threshold for a perceptron that computes
the logical and function i.e, must satisfy
Do the same for the logical or function .
The output of one neuron can be used as input for other neurons in a potentially extremely complicated network: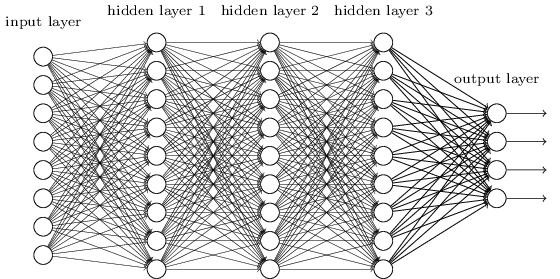
Is it possible to find a perceptron , such that
What if you are allowed to use a neural network composed as (one hidden layer)
 ?
?
Mathematically there is no reason to use special functions such as perceptrons in each node. One also uses
a (smooth) version of the perceptron employing the sigmoid function.
With the notation above, this function is given as
However, around 2011 it was observed that the perceptron activation function (ReLU) as defined in (1.19) led to better training
of deep neural networks. It is today, the most popular activation function.