6Convex functions

In this chapter we will dive deeper into convex functions. The main focus will be convex functions defined on intervals (convex subsets) of the real numbers i.e. convex functions in just one variable. Along the way, differentiability is introduced along with several classical results. We will sketch surrounding ideas, but skip proofs of some of the main results. In this chapter $\log(x)$ denotes the logarithm with base $e$ .

Mentimeter

Refresher

6.1 Strictly convex functions

Below we strengthen Definition 4.23 of a convex function.

Let $C \subseteq \mathbb{R}^d$ be a convex subset. A strictly convex function is a convex function $f: C\rightarrow \mathbb{R}$ , such that

$f((1 - t) x + t y) < (1-t) f(x) + t f(y)$ for every number $t$ with $0< t < 1$ and $x\neq y$ .

Strictly convex function. The line segment between $(x, f(x))$ and $(y, f(y))$ lies strictly ( $<$ ) above the graph of $f$ .

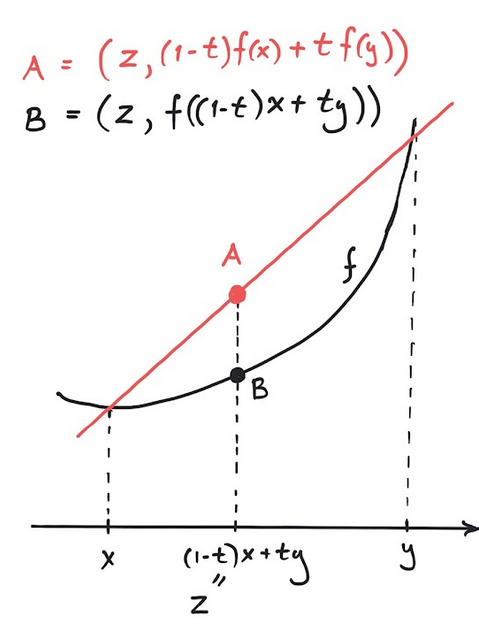
Consider the line (function) $f:\mathbb{R}\rightarrow \mathbb{R}$ given by

$f(x) = a x + b$ for $a, b\in \mathbb{R}$ . This function is convex, since we can formally write for every $t\in \mathbb{R}$ :

$\begin{aligned} f((1-t) x + t y) &= a ((1-t) x + t y) + b \\ &= a ((1-t) x) + (1-t)b + a (t y) + t b\\ &= (1-t)(a x + b) + t(a y + b)\\ &= (1-t) f(x) + t f(y). \end{aligned}\tag{6.1}$ However, the computation in (6.1) also shows why there is no chance that $f(x)$ is strictly convex. Intuitively, the graph of convex functions need to bend and curve a bit to be strictly convex. No lines should occur in their graphs.

Let $f$ be a convex function. Show $f$ is strictly convex if and only if

$f((1-t) x + t y) = (1-t) f(x) + t f(y)$ for $0 < t < 1$ implies that $x=y$ .

Give an example of a non-constant convex function $f:\mathbb{R}\rightarrow \mathbb{R}$ , which is not strictly convex. Show in details that $f(x) = x^2$ is a strictly convex function.

Hint

Look back to the relevant part of Exercise 4.25 for dealing with $f(x) = x^2$ .

6.2 Why are convex functions interesting?

We begin this section by giving the following result without proof.

A convex function defined on an open convex subset is continuous.

Give an example showing that Theorem 6.6 is not true if the convex function is defined on a closed convex subset.

Hint

Try to come up with an example like $f: [0, 1] \rightarrow \mathbb{R}$ . Look at the end point $0$ .

Hint

Well, try out

$f(x) = \begin{cases} 1&\text{if } x = 0\\ x&\text{if } x > 0 \end{cases}$

Let us now define precisely what is meant by a local vs a global minimum for a function.

Let $f: S\rightarrow \mathbb{R}$ be a function, where $S\subseteq\mathbb{R}^d$ is an arbitrary subset (not necessarily convex, open or closed). Then $x_0\in S$ is called a local minimum for $f$ if

$f(x_0)\leq f(x)$ for every $x\in S$ , which is sufficiently close to $x_0$ . Being sufficiently close to means that $x\in S$ satisfies

$| x - x_0 | < \epsilon$ for some fixed $\epsilon > 0$ .

In a much stronger notion, $x_0\in S$ is called a global minimum if

$f(x_0) \leq f(x)$ for every $x\in S$ (not just locally).

Graph of function defined on an interval. This function has a local minimum, which is not a global minimum.

Give an example of a local minimum that is not a global minimum for a precisely specified function. Also give an example of a global minimum, which is not uniquely defined (again for a precisely specified function). Uniquely defined means that there is precisely one $x_0$ , such that $f(x_0)$ is minimal.

We might as well have talked about maximum instead of minimum above.

Reformulate Definition 6.8 in order to define a local and a global maximum.

A local extremum is a point $x_0\in S$ , which is either a local minimum or a local maximum.

Convex functions $f: C\rightarrow \mathbb{R}$ are interesting, because of the local nature of the minimization problem

$\begin{aligned} &\text{Minimize} &f(x)\\ &\text{with constraint}\\ &&x\in C \end{aligned}\tag{6.2}$

If you run into a local minimum in (6.2), then you are sure that it also is a global minimum! This is the content of the result below.

Let $f: C\rightarrow \mathbb{R}$ be a convex function defined on a convex subset $C\subseteq \mathbb{R}^d$ . If $x_0\in C$ is a local minimum, then $x_0$ is a global minimum. If $f$ is strictly convex, then a global minimum for $f$ is unique.

By the definition of local minimum in Definition 6.8, there exists $\epsilon > 0$ , such that $f(x_0)\leq f(x)$ , when $x \in C$ and $\left\vert x - x_0 \right\vert< \epsilon$ . Suppose that $x_0$ is not a global minimum. Then there exists $x_1\in C$ with $f(x_1) < f(x_0)$ . Consider the point

$x_t = (1 - t) x_0 + t x_1\in C,$ where $0 < t < 1$ . Then

$f(x_t) \leq (1-t) f(x_0) + t f(x_1) < (1-t) f(x_0) + t f(x_0) = f(x_0).$ Since $\left\vert x_t - x_0 \right\vert = t \left\vert x_1 - x_0 \right\vert$ , we can choose $t > 0$ sufficiently small such that $\left\vert x_t - x_0 \right\vert < \epsilon$ implying $f(x_0)\leq f(x_t)$ , since $x_0$ is a local minimum. This contradicts that $f(x_t) < f(x_0)$ for every $0 < t < 1$ . Let $f$ be strictly convex and let $x_0$ be a global minimum for $f$ . If $x_1\in C$ , $x_1\neq x_0$ and $f(x_1) = f(x_0)$ , then

$f((1-\lambda) x_0 + \lambda x_1) < (1-\lambda) f(x_0) + \lambda f(x_1) = f(x_0)$ for $0 < \lambda < 1$ . This would contradict that global minimality of $x_0$ , since $x_0\neq (1-\lambda)x_0 + \lambda x_1\in C$ for $0< \lambda < 1$ .

The following little result turns out to be very useful and also very intuitive and drawable! It is a key component in characterizing convex differentiable functions $f(x)$ in terms of $f''(x)$ . We will not give the proof here.

Let $f:[a,b]\rightarrow \mathbb{R}$ be a convex function. Then

$\frac{f(x) - f(a)}{x - a} \leq \frac{f(b)-f(a)}{b - a} \leq \frac{f(b)-f(x)}{b - x}$ for $a < x < b$ .

The result in Lemma 6.13 is depicted above. A formal proof can be given from first principles only using Definition 4.23.

6.3 Differentiable functions

To appreciate the depth of the notion of differentiability, you should read the story (joke, actually) in the second paragraph of section 8-2 in volume I of the famous Feynman Lectures on Physics. Below is a photograph of the master explainer in action.

6.3.1 Definition

Let $f:(a, b)\rightarrow \mathbb{R}$ be a function defined on the open interval $(a, b)\subset \mathbb{R}$ . The notion of $f$ being differentiable at a point $x_0\in (a, b)$ can be glanced from the drawing below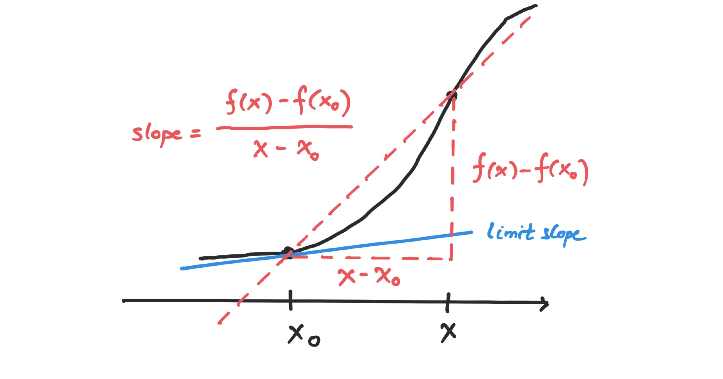

where we informally let $x$ approach $x_0$ and look at the limiting value of the slope. Newton used to say many hundred years ago, that the derivative of $f$ at $x_0$ is the value of this slope just before $x$ becomes $x_0$ . In modern day mathematical (obfuscated?) parlance, this gets translated into the following.

The function $f$ is differentiable at $x_0$ if there exists a number $c\in \mathbb{R}$ , such that for every $\epsilon > 0$ there exists $\delta$ with
$\left| \frac{f(x) - f(x_0)}{x-x_0} - c \right| < \epsilon \tag{6.3}$ for every $x$ satisfying $|x-x_0 |<\delta$ .

We will use a somewhat more operational definition below in terms of continuous functions $\epsilon$ defined around $0$ with $\epsilon(0) = 0$ . This looks difficult, but it is actually a clever way of approaching differentiability (and more in the spirit of Newton).

The function $f: (a, b)\rightarrow \mathbb{R}$ is differentiable at $x_0\in (a, b)$ if there exists

$c\in \mathbb{R}$
$\delta > 0$ with $x_0 - \delta, x_0 + \delta\in (a, b)$ i.e., $a + \delta < x_0$ and $x_0< b-\delta$ .
A function $\epsilon: (-\delta, \delta) \rightarrow 0$ continuous at $0$ with $\epsilon(0) = 0$ ,

such that

$f(x_0 + h) - f(x_0) = c h + \epsilon(h) h \tag{6.4}$ for every $h\in (-\delta, \delta)$ .

The number $c$ is denoted $f'(x_0)$ and called the derivative of $f$ at $x_0$ ; $f$ is called differentiable if it is differentiable at every $x_0\in (a, b)$ .

If a function $f:(a, b)\rightarrow \mathbb{R}$ is differentiable, we get a new function $f':(a, b)\rightarrow \mathbb{R}$ giving the (first) derivative at a point as output. We may ask again if this function is differentiable. If this is so, we may define a function $f'':(a, b)\rightarrow \mathbb{R}$ given by $f''(x) = (f')'(x)$ called the second derivative. This procedure may be continued. We use the notation $f^{(n)}$ for the $n$ -th derivative.

Let us apply Definition 6.15 to the function $f(x) = x^2$ at the point $x_0$ . Here

$f(x_0 + h) - f(x_0) = (x_0 + h)^2 - x_0^2 = 2 x_0 h + h^2.$ Here you immediately see that $c = f'(x_0) = 2 x_0$ with $\epsilon(h) = h$ (and $\delta = \infty$ ) in Definition 6.15.

Use Definition 6.15 to formally show that $f'(x) = 3 x^2$ if $f(x) = x^3$ .

In operating with differentiable functions you are supposed to draw on your previous knowledge. I have summarized some of this knowledge below (even though we will give hints below as how to prove some of the rules).

If $f(x) = a g(x)$ , where $a\in \mathbb{R}$ , then
$f'(x) = a g'(x)$ .
If $f(x) = x^n$ , where $n \in \mathbb{N}$ , then
$f'(x) = n x^{n-1}.$
If $f(x) = e^x$ , then
$f'(x) = f(x) = e^x.$
If $f(x) = \log(x)$ , then
$f'(x) = 1/x.$
If $f(x) = \sin(x)$ , then
$f'(x) = \cos(x).$
If $f(x) = \cos(x)$ , then
$f'(x) = -\sin(x).$
If $f(x)$ and $g(x)$ are differentiable functions, then the derivative of their product is
$(f g)'(x) = f'(x) g(x) + f(x) g'(x).$
If $f(x)$ and $g(x)$ are differentiable functions, then the derivative of their quotient is
$\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) g(x) - f(x) g'(x)}{g(x)^2}.$
If $f(x)$ and $g(x)$ are composable differentiable functions, then the derivative of their composite is
$(f\circ g)'(x) = f'(g(x)) g'(x).$

Suppose that $f(x) = \sin(x)$ . What is

$f^{(17)}(x)?$

6.3.2 Recall the derivative of a product?

From high school you know that the derivative of a product of two functions $f$ and $g$ is given by the formula

$(f g)'(x) = f'(x) g(x) + f(x) g'(x). \tag{6.5}$

We can use the $\epsilon$ -definition (6.4) to derive the product rule in (6.5). The computation below is a bit cumbersome, but actually quite doable. We assume to begin with that $f$ and $g$ are differentiable at $x_0$ according to (6.4) i.e.,

$\begin{aligned} f(x_0 + h) &= f(x_0) + f'(x_0)h + \epsilon_f(h) h\\ g(x_0 + h) &= g(x_0) + g'(x_0)h + \epsilon_g(h) h.\\ \end{aligned}$ Then we start the computation:

$\begin{aligned} &(f g)(x_0 + h) = f(x_0 + h) g(x_0 + h) =\\ &(f(x_0) + f'(x_0)h + \epsilon_f(h) h)\,\, (g(x_0) + g'(x_0) h + \epsilon_g(h) h) =\\ &f(x_0) g(x_0) + (f'(x_0) g(x_0) + f(x_0) g'(x_0)) h + \epsilon(h) h, \end{aligned}\tag{6.6}$ where the function

$\epsilon(h) = f(x_0) \epsilon_g(h) + f'(x_0) g'(x_0) h + f'(x_0) \epsilon_g(h) h + \epsilon_f(h) g'(x_0) + \epsilon_f(h) g'(x_0) h + \epsilon_f(h) \epsilon_g(h) h \tag{6.7}$ is seen to be continuous at $h=0$ with $\epsilon(0) = 0$ . The end result of this computation shows that $f g$ is differentiable at $x_0$ with

$(f g)'(x_0) = f'(x_0) g(x_0) + f(x_0) g'(x_0) \tag{6.8}$ again according to (6.4).

Show that the $\epsilon$ function defined in (6.7) satisfies the relevant conditions in Definition 6.15.

The formula for the derivative of a fraction i.e.,

$\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) g(x) - f(x) g'(x)}{g(x)^2}$ can be derived using a neat little trick. This is the topic of the following exercise.

Show how the product rule may be used to derive the rule for finding the derivative of a fraction:

$\left(\frac{f}{g}\right)'(x_0) = \dfrac{f'(x_0) g(x_0) - f(x_0) g'(x_0)}{g(x_0)^2}.$

Hint

$f'(x) = \left(g(x) \left(\frac{f(x)}{g(x)}\right)\right)'.$

6.3.3 Recall the one variable chain rule?

The formula for the derivative of a composite function is given by

$(f\circ g)'(x_0) = f'(g(x_0)) g'(x_0),$ where $g(x_0)$ is in the domain of $f$ . Let us see how (6.4) applies in showing this.

Suppose that $f$ is differentiable at $g(x_0)$ and $g$ is differentiable at $x_0$ , then we can mess around a bit with the $\epsilon$ -functions for $f$ and $g$ for the composite function $f(g(x))$ around $x_0$ :

$\begin{aligned} f(g(x_0 + h)) &= f(g(x_0) + g'(x_0) h + h \epsilon_g(h))\\ &= f(g(x_0)) + f'(g(x_0)) g'(x_0) h + \epsilon(h) h, \end{aligned}$ where (take a deep breath)

$\epsilon(h) = f'(g(x_0)) \epsilon_g(h) + \epsilon_f(g'(x_0) h + \epsilon_g(h)h) g'(x_0).$ Here $\epsilon$ is seen to be continuous at $0$ with $\epsilon(0)=0$ i.e., the composition $f(g(x))$ is differentiable at $x_0$ with derivative

$(f\circ g)'(x_0) = f'(g(x_0)) g'(x_0). \tag{6.9}$

The formula (6.9) is extremely important and useful. We give some applications in the exercises below.

For the function $f(x) = x^n$ for $n\in \mathbb{N}$ , you already know that $f'(x) = n x^{n-1}$ . Show that if you define the function $g: \{x\in \mathbb{R} \mid x > 0\} \rightarrow \mathbb{R}$ by

$g(x) = x^a := e^{\log(x) a},$ for an arbitrary number $a\in \mathbb{R}$ , then $g'(x) = a x^{a-1}$ .

Compute the derivative of the function $f: (0, \pi) \rightarrow \mathbb{R}$ given by

$f(x) = \dfrac{1}{\sqrt{\sin(x)}}$ using only paper and pencil! You can check your result afterwards using a computer.

Suppose that $g$ and $f$ are inverse functions i.e.,

$f(g(x)) = x\qquad \text{and} \qquad g( f(x)) = x.$ If you know the derivative of $f$ , how can you use the chain rule to get the derivative of $g$ ? Illustrate with examples like $f(x) = x^2$ and $g(x) = \sqrt{x}$ , $f(x) = e^x$ and $g(x) = \log(x)$ .

Suppose that $f:\mathbb{R}\rightarrow \mathbb{R}$ is a convex function. We know that $f$ is continuous, but is $f$ differentiable at every point $x_0\in \mathbb{R}$ ?

Hint

Nope. This is wrong. Come up with a convex function $f$ and a point $x_0$ , such that $f$ is not differentiable at $x_0$ .

6.3.4 The Newton-Raphson method for finding roots

We begin this section with a surprising example.

Suppose that $a> 0$ and we wish to compute $\sqrt{a}$ . To do this we may focus on the quadratic equation $f(x) = x^2 - a = 0$ and attempt to compute an approximate value $x_0\geq 0$ , such that $f(x_0)$ is close to $0$ . Let me at this point disclose that there is a very effective iterative scheme for doing this. You start by putting $x_0 = a$ and then iterate using the formula

$x_{i+1} = \frac{1}{2}\left(x_i + \frac{a}{x_i}\right) \tag{6.10}$ to get better and better approximations $x_0, x_1, x_2, \dots$ to $\sqrt{a}$ .

The formula in (6.10) is derived from

$x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)},$ where $f(x) = x^2 - a$ .

You can try out (6.10) below.

I have been in complete awe of the Newton-Raphson method since my early youth. It is an algorithm, where the notion of differentiability really shines.

The method comes from Definition 6.15 with $h = x - x_0$ : we are assuming that $x_0$ is very close to $x$ , where $f(x) = 0$ . Then

$f(x) - f(x_0) = f'(x_0) (x- x_0) + \text{a very small number}.$ Ignoring the very small number and solving this equation for $x$ we get

$x = x_0 - \frac{f(x_0)}{f'(x_0)}.$

In the Sage window below, I have entered the algorithm starting in $x_0 = 0$ running ten iterations for finding a zero for $f(x) = \cos(x) - x$ .

Graph

Give an example, where the Newton-Raphson method cycles between points and never finds the desired zero. Perhaps a drawing will help here.

The Newton-Raphson converges rapidly in most cases. Of course, it breaks down violently if it runs into a critical point i.e., a point $x$ , such that $f'(x) = 0$ .

William Cook has made some nice Sage code available for experimentation with Newton's method.

The formula (see button in Example 1.60) for the (monthly) payment $Y$ on a (car) loan over $N$ payments with a down payment of $P$ and an interest rate of $r$ (per payment or term) is given by the formula

$Y = \frac{r P}{1 - \left(\frac{1}{1+r}\right)^N}.$ There is no explicit formula for calculating $r$ given $Y, P$ and $N$ . Here the Newton-Raphson method is invaluable for estimating $r$ by approximating a zero for the function

$r(x) = Y - \frac{x P}{1 - \left(\frac{1}{1+x}\right)^N}.$

Your bank promises you a loan of $1.000.000$ DKK with yearly payments of $45.000$ DKK over $30$ years. At the same time it claims that its interest rate is very favorable at only $1.0$ %. Here the bank is wrong! What is the real interest rate? How much money do you save (compared to the original offer from the bank) if you insist that the bank offers you the promised interest rate of $1.0$ %?

6.3.5 Critical points and extrema

A critical point for a differentiable function $f:(a, b)\rightarrow \mathbb{R}$ is a point $x_0\in (a, b)$ with

$f'(x_0) = 0.$

The crucial result here is the following. It seems to date back to Fermat (see Fermat's theorem).

Let $f : (a, b)\rightarrow \mathbb{R}$ be a differentiable function. If $x_0$ is a local extremum for $f$ , then $x_0$ is critical point i.e., $f'(x_0) = 0$ .

Suppose that $\xi$ is a local maximum and that

$f(\xi + h) - f(\xi) = f'(\xi) h + \epsilon(h) h$ according to (6.4). If $f'(\xi)>0$ , then we can choose $\delta >0$ sufficiently small, such that $\left\vert \epsilon(h) \right\vert < f'(x_0)$ if $0\leq h < \delta$ , since $\epsilon(0) = 0$ and $\epsilon$ is continuous in $0$ . Therefore

$f(\xi + h) - f(\xi) = (f'(\xi) + \epsilon(h)) h > 0,$ contradicting that $\xi$ is a local maximum. The proof is similar for $f'(\xi) < 0$ and if $\xi$ is a local minimum.

Is the converse of the above lemma true i.e., if $f'(x_0) = 0$ is $x_0$ a local extremum?

Theorem 6.34 below is called the mean value theorem. It is a consequence of Lemma 6.32 and the extremely important Theorem 5.77 about continuous functions on compact subsets attaining their maxima and minima!

Let $f:[a, b]\rightarrow \mathbb{R}$ be continuous and differentiable on $(a, b)$ . Then there exists $x_0\in (a, b)$ such that

$f'(x_0) = \frac{f(b) - f(a)}{b - a}.$

6.3.6 Increasing functions

The definition below is much simpler than the definition of differentiability.

A function $f:S\rightarrow \mathbb{R}$ with $S\subseteq \mathbb{R}$ is called increasing if

$x\leq y\Rightarrow f(x) \leq f(y)$ and strictly increasing if

$x< y\Rightarrow f(x) < f(y)$ for $x, y\in S$ .

Give an example of an increasing function. Give an example of an increasing function that is not strictly increasing.

The following very important result is a consequence of Theorem 6.34. You probably already know this result from your previous (danish) education (monotoniforhold!).

Let $f : (a, b)\rightarrow \mathbb{R}$ be a differentiable function. Then $f$ is increasing if and only if $f'(x)\geq 0$ for every $x\in (a, b)$ . If $f'(x)> 0$ for every $x\in (a, b)$ , then $f$ is strictly increasing.

Show that $f(x) = x^3$ is strictly increasing i.e.,

$x < y \implies x^3 < y^3.$ Hint

$y^3 - x^3 = (y - x) (y^2 + x y + x^2),$ but why is $y^2 + x y + x^2$ always $> 0$ except when $x = y = 0$ ?

Suppose that $f: [a, b] \rightarrow \mathbb{R}$ is a continuous function, such that $f$ is differentiable on the open interval $(a, b)$ . Is $f$ increasing on $[a, b]$ if $f'(x)\geq 0$ for every $x\in (a, b)$ ?

Is it possible for a strictly increasing function $f: \mathbb{R} \rightarrow \mathbb{R}$ to be bounded i.e., does there exist a (positive) number $M$ , such that $|f(x)| \leq M$ for every $x\in \mathbb{R}$ ?

Hint

Have a look at

$f(x) = \dfrac{1}{1 + e^{-x}}.$

6.4 Taylor polynomials

If $x_0$ is a critical point for $f$ we cannot conclude that $x_0$ is a local extremum. We know that $f'(x_0)=0$ and we can get more information out of $f$ by exploring the signs of

$f''(x_0), f'''(x_0), \dots$

Suppose that

$f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n$ is a polynomial, then

$f(x) = f(0) + f'(0) x + \frac{f''(0)}{2} x^2 + \cdots + \frac{f^{(n)}(0)}{n!} x^n. \tag{6.11}$

For nice functions like $f(x) = e^x$ we can play this game ad infinitum. In fact in this way we get the beautiful infinite series

$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \cdots + \frac{x^n}{n!} + \cdots.$

If $f$ is an $n$ times differentiable function defined at $0$ , we call the polynomial in (6.11) the Taylor polynomial about the point $0$ of degree $n$ associated with the $f$ . Similarly, one may also define the Taylor polynomial of order $n$ about a point $a$ by

$f(a) + f'(a) (x-a) + \frac{f''(a)}{2} (x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!} (x-a)^n.$ Taylor polynomials can be used to approximate more complicated functions such as $\cos(x)$ and $\sin (x)$ with a well defined error term. This is cool classical mathematics. Unfortunately we do not have time to go deeper into Taylor's theorem, which states this in precise terms.

Compute the Taylor polynomial for $f(x) = \cos(x)$ up to degree $10$ .

Suppose you have a number $i$ that satisfies

$i^2 = -1.$ Can you make sense of the formula

$e^{i x} = \cos(x) + i \sin(x)$ using Taylor polynomials?

In the context of optimization, the following result becomes important. We will not give the proof, but only notice that Theorem 6.34 also here plays an important role.

Let $x_0$ be a critical point of an $n+1$ times differentiable function $f:(a, b)\rightarrow \mathbb{R}$ , such that $f^{(n+1)}$ is a continuous function,

$\begin{aligned} f''(x_0) &= 0\\ f'''(x_0) &= 0\\ &\vdots\\ f^{(n-1)}(x_0) &= 0 \end{aligned}$ and $f^{(n)}(x_0)\neq 0$ . If $n$ is even, then $x_0$ is a local minimum if $f^{(n)}(x_0) > 0$ and a local maximum if $f^{(n)}(x_0)<0$ . If $n$ is odd, then $x_0$ is not a local extremum.

Let us apply Theorem 6.43 to the function

$f(x) = a x^2 + b x + c,$ where $a\neq 0$ . Here $f'(x) = 2 a x + b$ and

$x_0 = - \frac{b}{2 a}$ is a critical point (why?). Since

$f''(x_0) = 2 a,$ we see that $x_0$ is a local minimum if $a > 0$ and a local maximum if $a < 0$ .

Have you seen Example 6.44 elsewhere, perhaps in a more geometric setting? What type of curve is the graph of $f(x)$ ? Here you may consult your previous mathematical knowledge.

What is the outcome, when you apply Theorem 6.43 to the function $f(x) = x^3$ at $x_0 = 0$ ?

Show that $x_0=0$ is a critical point of the function $f: (-\frac{1}{2}, \infty)\rightarrow \mathbb{R}$ defined by

$f(x) = e^x + \log(1 + 2 x) - 3 x.$ Use Theorem 6.43 in deciding if it is a local maximum or minimum or neither.

6.5 Differentiable convex functions

The following theorem is proved using Lemma 6.13 and Theorem 6.34. It immediately implies Corollary 6.48, which is the result mostly used.

Let $f:(a, b)\rightarrow \mathbb{R}$ be a differentiable function. Then $f$ is convex if and only if $f'$ is increasing. If $f'$ is strictly increasing, then $f$ is strictly convex.

Theorem 6.47 leads to the following all important result.

Let $f:(a, b)\rightarrow \mathbb{R}$ be a twice differentiable function. Then $f$ is convex if and only if $f''(x)\geq 0$ for every $x\in (a, b)$ . If $f''(x) > 0$ for every $x\in (a, b)$ , then $f$ is strictly convex.

Wait! Stop! Why did I not write $f''(x) > 0$ if and only if $f$ is strictly convex?

Mentimeter

Zooming in on $f(x) = x^3$

You cannot deduce from Corollary 6.48 that the function $g: \mathbb{R} \rightarrow \mathbb{R}$ given by $g(x) = x^4$ is a strictly convex function. Why not?

You can deduce from Corollary 6.48 that $f(x) = x^2$ is a strictly convex function. How can $g(x) = f(x)^2$ be used to prove that $g(x)$ is a strictly convex function?

Show that $f(x) = e^x$ is a strictly convex function $f: \mathbb{R}\rightarrow \mathbb{R}$ .

Show that $f(x) = -\log(x)$ is a strictly convex function $f: (0, \infty) \rightarrow \mathbb{R}$ .

Show that $f: \{x\in \mathbb{R} \mid x \geq 0\}\rightarrow \mathbb{R}$ given by

$f(x) = -\sqrt{x}$ is a strictly convex function.

Another nice application of Lemma 6.13 (and Theorem 6.47) is the following.

Let $f:(a, b)\rightarrow \mathbb{R}$ be a differentiable function. Then $f$ is convex if and only if

$f(y) \geq f(x) + f'(x)(y-x)$ for every $x, y\in (a, b)$ .

Suppose that $f:(a, b)\rightarrow \mathbb{R}$ is a differentiable convex function and $x_0\in (a, b)$ is a critical point for $f$ . What can you say about $x_0$ using Theorem 6.53?