2Linear equations
Try to come up with a solution to
(2.1)
i.e., find
numbers satisfying all three equations. Do not use a computer.
Is there more than one solution?
Write down two linear equations with two unknowns, which do not
have a solution.
2.1 One linear equation with one unknown
Point out the mistake(s) in the
argument
This teaser was presented at the workshop for new teaching assistants, August 2020.
below showing that .
A saline solution is a mixture of % sodium chloride in water. Suppose that you have
liters of water containing % sodium chloride. How many liters of
distilled water ( percent sodium chloride)
do you need to add to get a saline solution.
liter
liter
liter
Diophantus's youth lasted of his life. He grew a beard after more. After more
he got married. Five years later he had a son. The son lived half as long as the father
and Diophantus died four years after the son. At what age did Diophantus die?
Link/Hint
You can read about Diophantus and the solution to the puzzle in the Wikipedia entry about him. Please
try solving the problem on your own first.
2.2 Several linear equations with several unknowns
2.2.1 Several equations
To be completely precise about these steps, let us use predicate logic. A solution to the system of
equations above is a pair of numbers satisfying the predicate
Now use the rules in Proposition
1.12
and substitution to rewrite
systematically:
Tracing back we have actually proved that
Why is the only solution to the equations in
(2.2)
? How can we be
so sure that there are no other values for and satisfying
(2.2)
?
Kona coffee is a delicacy priced at kroner for grams.
A standard gram bag of Arabica beans is priced at kroner.
A merchant wishes to mix coffee beans of these sorts aiming for a price of
kroner for grams. Which one of the percentages below
comes closest to the content of Kona coffee in the mixture?
2.3 Gauss elimination
Suppose that
are two linear equations in the unknowns with
. The equation gotten by first isolating
in the first equation and then inserting in the second equation
is identical to the equation you get by adding the first equation multiplied
by to the second equation.
Isolating in the first equation inserted in the second equation gives
the equation
Adding multiplied to the first equation to the second equation gives
Using basic arithmetic you can see that
(2.4)
can be rewritten to
(2.5)
.
We wish to solve the system of equations
The first step is subtracting the third equation from the second:
Then we multiply the third equation by and subtract from the first:
Finally we add the second equation to the first:
We have now reduced the original system of equations
(2.6)
to
where the first equation shows that . Now can be inserted into
the second equation, giving , which is solved by .
Finally
and are inserted into the third equations giving the equation
, which is solved by .
One very important observation here is that and is the only
solution to
(2.6)
. This is a logical consequence of the
bi-implication arrows throughout the above calculations.
And you are to know, that by each Æquation one unknown Quantity may be taken away, and consequently, when there are as many Æquations and unknown Quantities, all at length may be reduc'd into one, in which there shall be only one Quantity unknown.'
There are three categories of corn. Three bundles of the first class, two of the second and one of the third make measures. Two of the first, three of the second, and one of the third make measures. Finally one of the first, two of the second and three of the third make measures. How many measures of graín are contained in one bundle of each class?'
How many solutions does the system of equations below have?
None.
Precisely one.
Infinitely many.
How many solutions does the system of equations below have?
Precisely one.
Precisely two.
Infinitely many.
Find the solutions to
by expressing and in terms of i.e., isolate on the
left hand side, such that
where indicate an expression only in the unknown .
Your enemy transmits secret codes consisting of four integers over the internet. He does
not transmit the code itself but an encrypted version given by
You have knowledge of the encryption method above and by listening in on
a recent communication, you learn that the encryption
was sent. What was the original secret code before the encryption?
Extra credit
Suppose that you only know that the encryption scheme is
and that you have no knowledge of the numbers .
How many transmissions do you need to know at the minimum to find
these encryption numbers?
The diagram below shows a network of roads and intersections.
Every road is labeled by a number indicating the average number
of cars per hour on the road. Some of these numbers
are unknowns. Write up a system of linear
equations for finding .
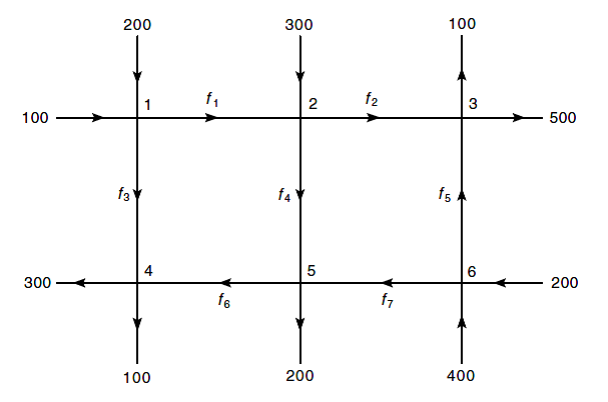 Compute
supposing that and .
Compute
supposing that and .

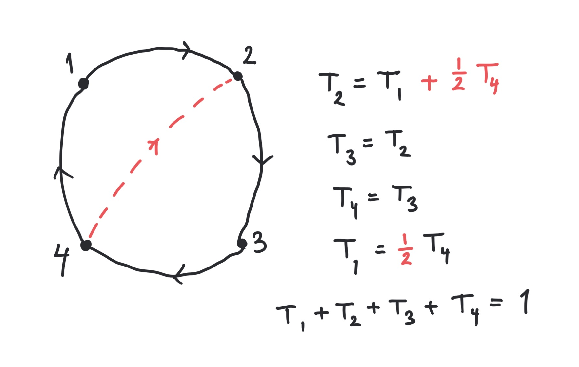
Which webpage in the above diagram loses most traffic when a link is added from to ?
You may try out the python code below to simulate a random tour
of the small internet in Example
2.15
.
The list (or matrix)
simulates a random surf with clicks starting in node .
The linear equations really seem to give the right result!
A = [[0,1,0,0], [0,0,0,1], [1,1,0,0], [0,0,1,0]]
simulate(0, 1000)
2.4 Polynomials
Suppose that
To compute it seems that you need multiplications
( and ) and additions.
Can you compute with only multiplications and additions?
Try to generalize to the computation of , where is a polynomial
of degree (you should only need multiplications and additions here).
2.4.1 Polynomial division
Watch the five minute video above and
carry out (do not use a computer) the polynomial division alluded to in
(2.8)
.
Let be a non-zero polynomial. Then
for every polynomial , there exists
polynomials , such that
where or .
We will prove this using induction on . Suppose that
In general if , then
satisfies the assumptions for the identity in
(2.9)
with
and .
If , then is a polynomial of
degree . So by induction we may find polynomials and , such that
Therefore
giving the desired result with and .
2.4.2 Roots of polynomials
A real number is a root of the polynomial if and only if
for some polynomial .
By Theorem
2.21
, we may write
where or is a non-zero polynomial of degree zero i.e., a non-zero
constant. Now the result follows, since
using
(2.10)
.
Is there an easy way of deciding if a polynomial of degree one divides
a polynomial without performing the (long) division of by
. Here divides means that for some polynomial .
Deriving the formula
(2.11)
comes from a classical algebraic trick called completing the square. Looking
at the quadratic equation , what bothers us is the term . If we could solve the equation rewriting to
and then taking square roots. The first step in this direction is rewriting
the equation
to
We would like to add a number to both sides of
(2.12)
so that the left hand side comes to look like
This is what is called completing the square.
Comparing the left hand side of
(2.12)
with the right hand side of
(2.13)
, we find that
works.
Therefore
(2.12)
implies
This identity can be rewritten into the formula
(2.11)
for solving the
quadratic equation.
A non-zero polynomial of degree can have at most roots.
We will prove this by induction starting with . Here
for and
Therefore has precisely one root. Suppose now that we have proved that
polynomials of degree has at most roots. Assume that
is a polynomial of degree . If has no roots,
we are done with the proof. Suppose that i.e.,
is a root in . Then
by Proposition
2.22
. Here has to be a polynomial of degree and
therefore by induction, has at most roots. However, if ,
then either or . We have proved that
cannot have more than roots.
Theorem
2.24
has a few interesting consequences. First it implies that two
identical polynomials i.e., for every must have
the same coefficients.
Secondly if two polynomials and of degree satisfy
for distinct points , then
.
In Remark
2.25
it is stated that if two polynomials and of degree satisfy
for distinct points , then
. How does this follow from Theorem
2.24
?
A polynomial of odd degree always has a root.
Compute (without using a computer!) the roots of the quartic
Give an example of a polynomial of degree with precisely one root.
Suppose that are two roots of the quadratic polynomial
How can and be computed in terms of and ?
Show concretely how this can be applied to the polynomial
: if you know that how can you easily
find the other root?
Show that and use this.
2.5 Applications of linear equations to polynomials
The two lines and have a single point
of intersection. Compute this point.
Give an example of two parallel lines and their equations.
Notice in
(2.16)
that
where (for example) is a polynomial of degree two satisfying
What about and with respect to and ?
Compute the polynomial you get when you apply
(2.16)
to and
. How do you explain this result in terms of the
points and plotted in plane?
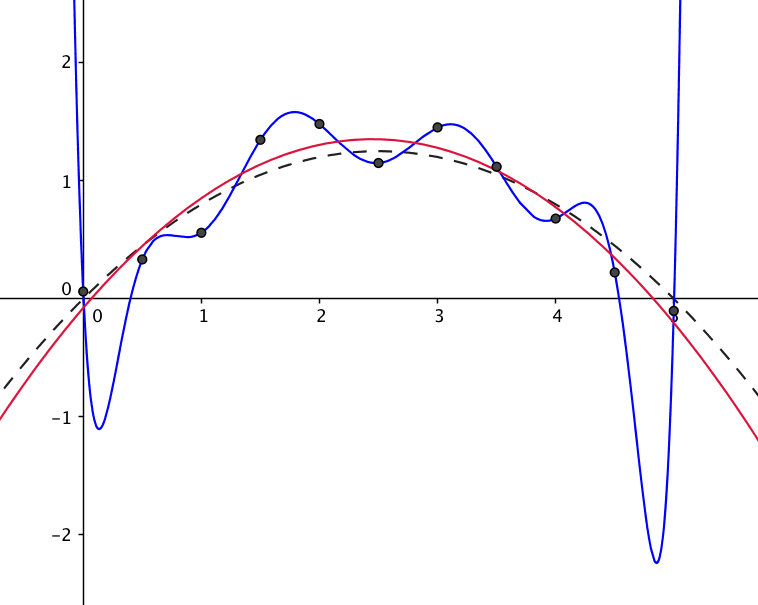
2.5.1 The magic of Lagrange polynomials
Let us explain with a simple numerical example what happens in
(2.16)
. Suppose we wish to find a polynomial through the
points
More precisely we wish to find numbers and , such that
This is a system of three linear equations which in this case has a unique solution in
and .
We may, however, attack this problem in another way. Suppose that and
are polynomials of degree at most two, such that
Then
really is the polynomial we wish to find.
The insight is that these and can be explicitly written down as
Compute so that
where
You can do this either by Lagrange interpolation or by solving linear equations. Which one
do you prefer?
2.6 Shamir secret sharing
A company needs to secure their vault's passcode. They could encrypt it, but what if the beholder of the secret key is unavailable or turns rogue?'One needs to distribute the secret. This is where SSS comes in. It can be used to encrypt the vault's passcode and generate a certain number of shares, where a certain number of shares can be allocated to each executive within the company. Now, only if they pool their shares can they unlock the vault. The threshold can be appropriately set for the number of executives, so the vault is always able to be accessed by the authorized individuals. Should a share or two fall into the wrong hands, they couldn't open the passcode unless the other executives cooperated.
You are in a study group consisting of four people. The
professor has decided that you submit your project using a
secret code that is distributed to the group members with Shamir
secret sharing. At least three group members need to agree on
submission.
On the day of the deadline three group members with shares
are present. What is the secret code they may use to submit their
project?
2.7 Fitting data