1The language of mathematics and prompting
1.1 The art of prompting

💬
Always answer in the context described below.
Context: I am taking a first semester college level course in introductory mathematics and optimization. Emphasis is on precision and small proofs in mathematics. Please give some conrete examples with mathematics involved.
- Tell me what a good and precise prompt is.
- Show me two examples of good prompts.
- What is a good prompt if I want to know about code written in Sage or python?
- What is a good prompt if I want to know how to enter some specific mathematics in LaTeX?
💬
Please solve the equation $x^2 - x - 1 = 0$. Guide me through the steps. Make sure that the underlying logic in your arguments is correct.
Study
the OpenAI guide on prompt engineering.
Then come up with prompts that make a chatbot act like a mathematics tutor for you.
Here is a small example that you may extend.
💬
Please act like a friendly tutor and teach me about the derivatives of simple functions. Test my understanding after each concept you explain.
Start your journey using the prompt below.
Come up with your own prompt for a question related to software.
💬
I am doing weekly exercises in mathematics at the college level. Please suggest a very simple template in
LaTeX for hand in of these exercises. Also, show me how to typeset an equation in LaTeX.
There seems to be a web interface to LaTeX called Overleaf. Please tell me how to access this so that I can
enter a weekly exercise.
Below I ask for feedback from the chatbot on some dubious chunk of mathematics.
Insert your own mathematics in notation and ask for feedback in a prompt.
💬
Please give feedback on the mathematics contained in the $\LaTeX$ below in triple quotes. Emphasize logic and precision.
"""
$$
x^2 = 1 \implies x = 1
$$
From this it follows that $1 + 1 = 3$.
"""
1.2 Black box warnings
💬
I am taking a first semester college level mathematics course spanning 14 weeks and 10 ECTS. One ECTS
amounts to 28 hours. The teaching activities every week amount to 4 hours of lectures,
2 hours of exercise sessions and 3 hours of study cafe. I expect that final exam will take 40 hours
of the 10 ECTS. Please schedule a weekly study plan for me along with a plan for the final exam.
1.3 Computer algebra (and python)
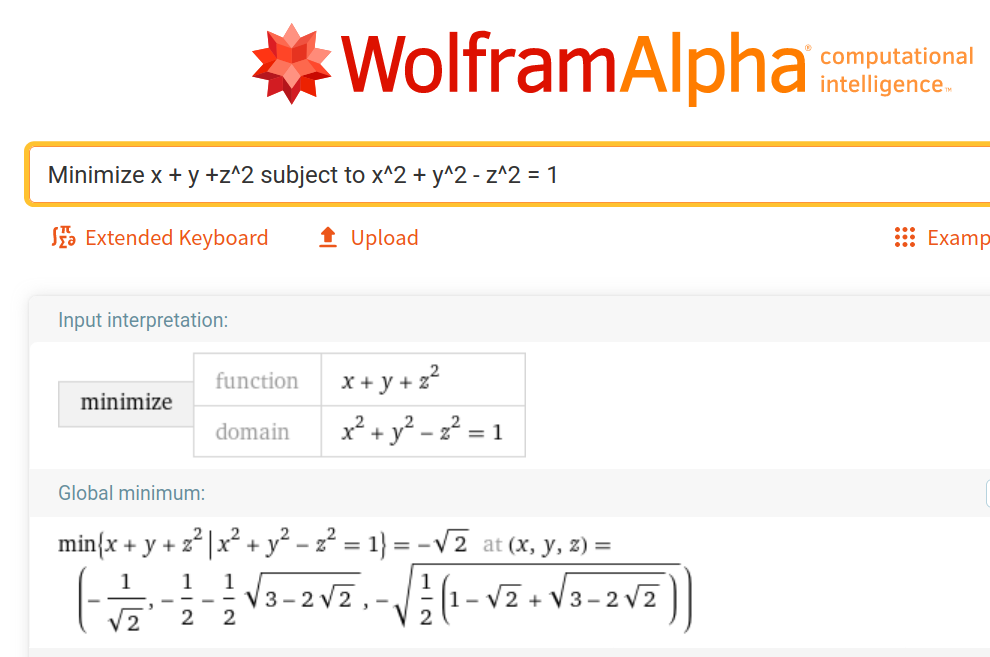
Prompt a chatbot with
and explain why the output from WolframAlpha is weird.
Use prompting to make it explain the mathematics input notation.
Finally use your own mental powers (and feedback from the
chatbot) to explain what the proper output should have been.
💬
What is
$$
-\sqrt{\frac{1}{2} (1 - \sqrt{2} + \sqrt{3 - 2\sqrt{2}})}
$$
💬
I am taking a mathematics course that uses the computer algebra system Sage.
The course uses the browser, where I can enter and run small snippets of code in Sage and python.
I have no/some/extensive prior programming experience.
Give me a brief introduction to Sage and explain how it relates to python.
Finish your reply with a small exercise I can do.
If no/some/extensive is present above in this prompt, remark this and only reply with
Please select your programming experience.
Did you notice that you can edit and enter new commands in the Sage window?
Do the following problems using Sage based on the Sage guided tour.
LLM
- Consider . Plot the graph of from to . Computing does not make sense. Do you see a way of assigning a natural value to using the graph?
- Find an approximate solution with four decimals to the equation .This is an example of an equation, that can only be solved numerically. Try first plotting the graph of from to . Then use a suitable function from the Sage guide.
- Compute with decimals.
Compute the sum
What is the elegant answer? Explain!
Bonus question
Generalize your answer/method to computing the sum
for .
1.4 Numbers
1.4.1 The natural numbers and the integers
The set of natural numbers is The set of integers is These are infinite sets, since they contain infinitely many elements as indicated by the dots1.4.2 The rational numbers
A rational number
consists of a numerator and a denominator .
If and . Then and
are considered equal i.e.,
if and only if .
So there are many different ways of representing a rational number, such as
Here
In fact, a fraction stays the same when its numerator and denominator are
multiplied by the same natural number.
Click on the right equalities below. Do not use Sage (or any computer)!
1.4.3 The real numbers
A real number is defined by
where and is an infinite sequence of integers (digits) in .
Explore using prompting the history of numbers in mathematics. Also make a chatbot
explain why a rational number must have a periodic decimal expansion.
1.4.4 Arithmetic rules for numbers
Suppose that is one of the sets or . Then for numbers
all in we have
- for some number .
- for some number .
Argue precisely that for using Proposition
1.12
.
We know that zero times any number is zero. Deduce this from the rules in
Proposition
1.12
starting with .
Verify that
(ⅵ)
is true for some specific non-zero numbers. Also
convince yourself that WolframAlpha actually
accepts space (between numbers and variables) as multiplication.
Suppose that and . It seems
that computing involves two multiplications and one addition. Multiplications are
expensive operations on a computer. Is there a way of computing
with only one multiplication and one addition?
Suppose that . Use the distributive law to show that
1.5 Propositional logic
Suppose that we are presented with four cards
with a (natural) number on the front and the color
blue or red on the back.
In
(1.5)
, the first and third cards are shown with their fronts facing up and
the second and fourth cards are shown with their backs facing up.
A claim (proposition) is made that if a card has an even number on the front, then it
must have the color blue on the back.
Your task is to verify this for the cards above. Of course you can
do this by turning all four cards, but is there a way of checking this
by turning less than four cards?
What if we add the claim, that if a card has the color
blue on the back, then
it must have an even number on the front?
Find two propositions and so that the claim reads
.
A prosecutor says to the defendant: "If you committed this crime you did not act alone".
Explain why the defendant should not answer "no, that is not true" here.
Explain why Python/Sage thinks that
the value
Thanks to Gerth Brodal for pointing this out to me
of
is False! Notice that you are dividing one by zero in the last "integer" above.
1.5.1 Propositional logic as a formal language
A proposition in the variables is an expression involving
the symbols that
can be generated using the rules below
- The variables are (atomic) propositions.
- If is a proposition, then is a proposition.
- If and are propositions, then , and are propositions.
The expression is a proposition. Let us see how it is generated
using the rules in Definition
1.22
.
- First, is a proposition using (ⅰ) .
- Then is a proposition by using (ⅱ) with , since we know by (1) that is a proposition.
- Since is a proposition by (ⅰ) , it follows that is a proposition using (ⅲ) with and , since we know by (2) that is a proposition.
- Finally, since is a proposition by (ⅰ) it follows by (ⅲ) with and that is a proposition, since we know by (3) that is a proposition.
According the generating rules in Definition
1.22
, which of the
following expressions are propositions in the variables .
1.5.2 Truth tables and equivalent propositions
The truth tables corresponding to the propositions and
are given below.
For example, if and , then
and
The notation is used frequently. It means that both
and are true i.e.,
1.5.3 Using Sage to compute truth tables
Construct by hand the truth table for the proposition
.
Convince yourself either using Sage or by writing out truth tables that
1.5.4 Variables, predicates and quantification
A predicate is a proposition depending on one or more variables.
If , then is true, whereas is false.
is a predicate in two variables and . Here is true, whereas is false.
For every and there exists
Here is a statement about real numbers
This statement reads: no matter which real number you pick, if ,
then . We definitely want this to be true. Being true means
that
(1.8)
must hold for all numbers , also ,
which reads
The above statement is an example of a false implies true statement, which
we want to be true.
In general terms, in proving the statement that holds for every in
some set , we are really only interested in for which is true, since
is our assumption. We still need to be true for for
which is false. This is assured by the truth table for , since
and are both true.
Which of the following are true?
1.5.5 Proofs and inference rules
1.5.6 The use of implication () and bi-implication ()
Prove that
for every (see Definition
1.69
with for the precise definition of ).
Write out every inference rule!
You need to be very precise here. What does mean precisely if ? In
Definition
1.69
you will see that it means that . From this
you need to deduce
Try out
💬
Is
$$
x \geq 0 \iff x^2 \geq 0
$$
a true statement? Give me 3 carefully crafted exercises
training me in distuishing $\implies$ and $\iff$.
Only use basic mathematics involving
numbers and arithmetic operations.
After each exercise stop, ask for the
answer and give valueable feedback and guidance.
1.5.7 More on mathematical proofs
An integer is called even if it is divisible by . So the even integers are
An integer is called odd if it is not even. So the odd integers are
Consider the
proposition:
where i.e., the square of an odd
integer is odd. This seems true for a first selection
of examples: .
What does it mean
exactly for a number to be odd? This means that it is
not divisible by or that there exists another
integer , such that . So
Therefore we need to show that
Notice that I had to change into in the second proposition above.
The two variables are not the same: is associated with and
is associated with .
Let us assume that . Now we need to argue that for some . You stare at this for a while
and notice that we should use the assumption in
computing :
Thus, using our assumption we may conclude that if , then
where . This completes the proof.
1.5.8 Proof by contradiction
An irrational number is a (real) number that is not rational. It is a
startling fact that such numbers exist, but they do! The square root of two
is an example.
We will prove that there exists two irrational numbers , such that
is rational.
Consider the proposition given
by
Either is true or false. If is true we are done putting . If not, then
must be false and is irrational. But then
and we are done putting and .
So which one is it? Is
rational or irrational?
This is really advanced mathematics based on the
Gelfond-Schneider theorem.
Let us use proof by contradiction to show that the proposition ( is an irrational number) is true.
Assuming that is false, we must have that is true. But
is the proposition (that is a rational number)
Here , where is the proposition
since we can assume that is not a common divisor of and by
Definition
1.7
.
However,
The last implication above follows from Exercise
1.36
. If is even, then
for some . Therefore and
so that is also even. We have proved that implies the proposition given by
Since we are assuming that is true, we must have that is false. However we have
shown that is true. But is a false. Therefore
we must have that is false and therefore that is false. But then
according to the law of the excluded middle, we must have that is true.
Consider the first prime numbers
Check that
are prime numbers by using the Sage window below (factor gives
the prime factorization of a natural number).
Is it true in general that
is a prime number?
Assume that we know that every natural number must be divisible by a prime number.
Prove that there are infinitely many prime numbers using proof
by contradiction.
Show how the
assumption that there are only finitely many prime numbers say
leads to a contradiction by using that the natural number
must be divisible by a prime number.
1.6 More on sets
1.6.1 Objects and equality
Click on the right equalities below.
You know that . Use Sage to find a similar identities
for and .
Go back and look at (the beginning of) Exercise
1.40
.
Two sets and are equal i.e., if they contain the same elements.
Give a precise reason as to why the two sets and are not equal.
Is it possible for a set with elements to be equal to a set with elements?
Come up with three lines of Sage code that verifies . Try it out.
The empty set
For some reason (perhaps a good one) python does not accept as input for the empty set.
Why is this? Evaluate the python snippet below and explain.
1.6.2 The symbols and
1.6.3 Subsets
List the subsets of . How many are there?
It turns out that the empty set is a subset of any set.
Explain why this is so using the definition of .
LLM
Below Sage (not python) will list all subsets of the set . Before pressing
the Compute button, try to write them down on your own.
List all the subsets of a set with five elements. In general, how many subsets does a set with elements have?
The set
is not a subset of
, simply because
does not belong to .
This exercise actually has
possible correct solutions.
The empty set has
elements. A set with
elements has
subsets. In general a set with
elements has
subsets.
1.6.4 Set-builder notation
Suppose that and
Then
This notation has found its way to several programming languages like list
comprehension in python.
List the elements in the following subsets.
Consider the predicate
Write
down the elements in
Is
an infinite set?
Explore the fascinating world of prime numbers and learn about twin primes.
You have previously encountered systems of linear equations like
The solutions to
(1.12)
can be identified with a subset of
. Define this subset precisely i.e., write the subset as
where is a predicate in the variables .
Suppose that and
Then write down precisely what is i.e., find suitable predicates in the
variable , such that
and
Consider the subset of pictured in the drawing below
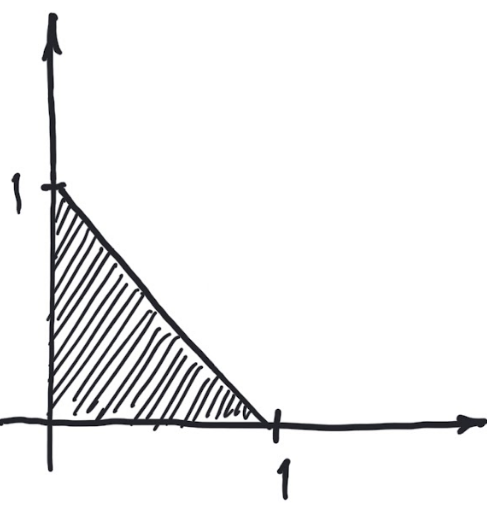 Express as
where are predicates in the variables .
Hint
Express as
where
and and are suitable predicates in the variables .
Express as
where are predicates in the variables .
Hint
Express as
where
and and are suitable predicates in the variables .

A predicate in the variables could be something like
1.6.5 Intersections, unions and the symbols and
You should experiment using the python window below to get a feeling for these three operations.
Suppose that , and . What is
?
Let , and . Verify by hand (no computer) that
- .
- .
- .
- .
Given two sets and , is it true that
and ?
What about ?
Suppose that and are two finite sets. Is it true that
What about
Seriously, both formulas are wrong. Can you come up with the correct
version of the formula for ?
Use your correct formula to find a formula for
viewing as the first set and as the second set. Here you need
the formula
Why is this formula true? Finally, explain why
Hint
If you are attacking the last part of this exercise using Exercise
UNDEFINED: logictt
, you
may find it useful to notice that two sets are equal i.e,
if and only if
Also,
There is one more operation called the symmetric difference between two sets and . It is
denoted . Experiment in the python window below to find out exactly what it does.
Is it true that ?
Let and denote sets. Which of the following are true?
For some sets and we can have
1.6.6 Pairs, triples and tuples
If and , then
Consider two pairs and each from in . When
is ?
The Cartesian product can be computed in python as shown below.
For a given set and we define the -fold cartesian product of as
Formally is the set of pairs , where . Is there a natural
way of drawing elements in ?
1.7 Ordering numbers
A subset of positive numbers in a set of numbers must satisfy
- For every one and only one of the following conditions must hold
- If , then and .
Notice that we only use arithmetic operations to define orders on
numbers in Definition
1.69
.
This is also how computers compare numbers algorithmically. Also if ,
putting makes all of the conditions in Definition
1.69
hold. If you are given an integer, it is , positive or negative. This is the
content of
(ⅰ)
in Definition
1.69
.
Also given two natural numbers, their product and sum are also natural numbers. This is
the content of
(ⅱ)
in Definition
1.69
.
Suppose that , where is a set of numbers and given
by a subset of positive numbers as in Definition
1.69
.
Prove that
1.7.1 Ordering
How is one supposed to interpret for example? Go ahead and formulate
(1.14)
correctly comparing only two integers at a time.
How does Python/Sage interpret ? Find out using the Sage snippet below.
What about ? What about ?
Assume that and that . Then drag and drop the
elements from the left to the right below to explain that
.
By assumption .
This means that
This means that
To show that , we need to show that
.
But . Therefore,
But . Therefore,
, since
1.7.2 Ordering
For ,
We must check when
This happens precisely when the numerator or . Therefore
the condition in the proposition is satsified.
Use proof by contradiction (see section
1.5.8
)
to show precisely that there does not
exist a smallest positive rational number.
Suppose that .
Order the arguments below so that they constitute a coherent explanation of the
statement that if
then
By definition this means that .
We are assuming that .
For integers we know that the rule
holds. Therefore
we need to show that .
Since and is a consequence of , we are
done if we know this is true.
However, this is a consequence of our assumption .
To show that
we need to argue that .
Similarly to the quiz above, assume that
Write down a precise argument showing that
On Twitter, Raman Gupta posted the note below
\begin{excluderag}
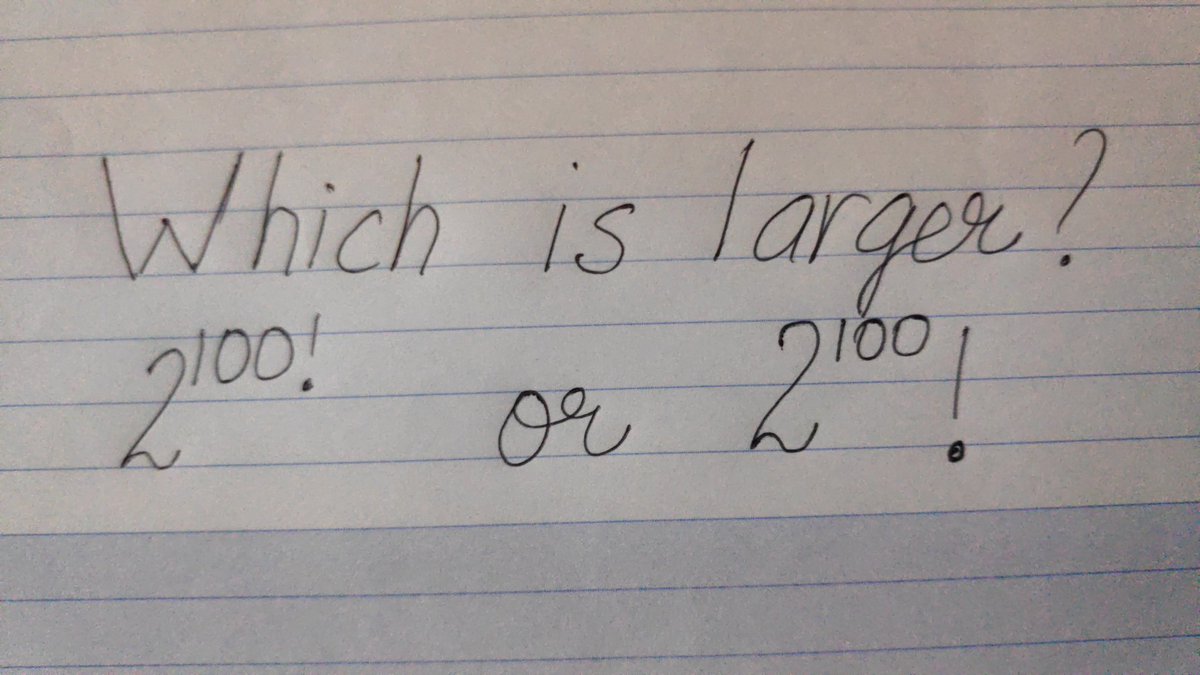 \end{excluderag}
For a natural number ,
For example, and . What is the answer for the
question in the note?
Experiment a bit with Sage: define a function , which computes
Then look at
\end{excluderag}
For a natural number ,
For example, and . What is the answer for the
question in the note?
Experiment a bit with Sage: define a function , which computes
Then look at
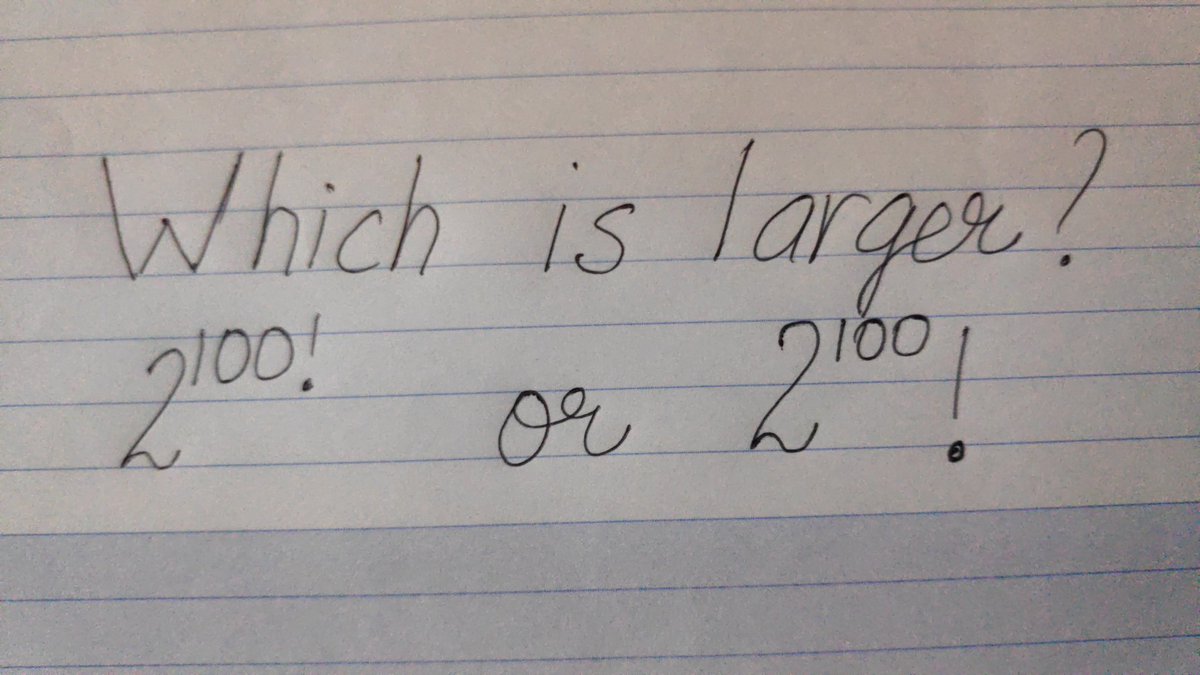
Can you spot the system in the fractions in the diagram below?
 Once you see the system, extend the diagram with the next level downwards. Is every
positive fraction present in this diagram if one keeps adding levels?
Once you see the system, extend the diagram with the next level downwards. Is every
positive fraction present in this diagram if one keeps adding levels?
Suppose that
and . Then for
we have and . If is
a positive fraction, such that
show that
1.7.3 Ordering
Given two distinct real numbers . Prove that
there exists a rational number , such that
1.8 Proof by induction
Suppose that are infinitely many propositions given by . Then
is true if
- is true.
- is true.
Suppose by contradiction that there exists , such that
is false. Then the subset
is non-empty. Therefore it has a first element .
Here , since is assumed to be true. So we
know that is true and that
is true. But the latter
implication is a contradiction, since true implies
false is false.
For a real number , the extremely useful formula
holds. Let us prove this formula by induction. For this amounts to the identity
which is true since . We let denote
the identity in
(1.17)
. We have seen that is true. The induction step
consists in proving . We can prove this
by adding to the right hand side in
(1.17)
:
Real life application
In order to pay for a house you borrow DKK at an interest of
per year. You want to pay off your debt over years by
paying a fixed amount each year. How much is the fixed yearly
amount you need to pay?
Let us analyze the setup: suppose that the fixed yearly amount
is . We will find an equation giving us in terms of
and . Put .
After one year you owe
After two years you owe
After three years you owe
In general after years you owe
Since we want to be debt free after years, the yearly payment will have to satisfy
By the formula
(1.17)
, we get
Here can be isolated giving the formula
With the current (August 2024) interest rate around four percent, you pay a fixed monthly
amount of around 4770 DKK (down from 5420 DKK in 2023, when the interest rate was five percent) for borrowing one million DKK over years.
Verify the computation (induction step) in
(1.18)
i.e., explain
the operations used to go from the left to the right of the two equalities.
Locate the mistake in the following fake induction proof of the curious fact that
for every .
Let be
the proposition . Then is true.
We wish to prove that assuming that are true:
This shows that and therefore that for every
.
Prove by induction that the sum of the first odd numbers is
given by the formula
i.e., for we have
Prove by induction that
Prove using the idea of induction that
for .
Prove the following by induction on : if items are put into containers and
, then at least one container must contain more than one item.
1.9 The concept of a function
To be completely fair, it is possible from Python 3.5 to add type annotations to functions, so that we could write
def f(n: int) -> int: return(n+1)
Mathematically a function takes values from a set and returns values in a set . In details,
it is denoted and the value associated with is denoted .
Here is called the domain of and is called the codomain of . Less,
formally is called the input set and the output set for .
Please notice that a function is a very, very general concept. It is not just something
that you draw as a graph on a piece of paper. Of course, you can draw a function
like :
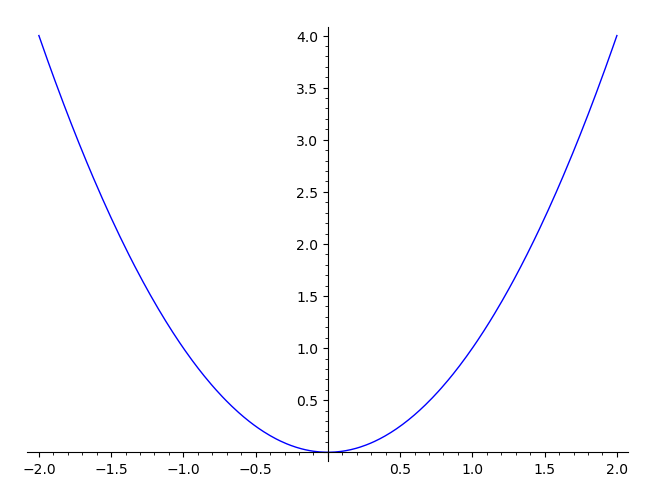 Generally, a function is given by a machine, formula or algorithm that
computes for every . Nothing more, nothing less. It really has nothing to
do with a graph (even though graphs can sometimes be useful for visualizing certain functions like ).
Generally, a function is given by a machine, formula or algorithm that
computes for every . Nothing more, nothing less. It really has nothing to
do with a graph (even though graphs can sometimes be useful for visualizing certain functions like ).

Good examples of functions can be found in the cryptographic hash functions. They are examples of complicated functions , where
is infinite and finite. Here could be data like plain text files and could be
a bit number. This is the setup for the widely used sha-256 cryptographic hash function.
The whole point of a cryptographic hash function is that it must be humanly impossible to
compute with given
A pair with is called a collision
.
In fact, sha-256 is used in the Bitcoin block chain. The precise definition of
sha-256 can be found in FIPS PUB 180-4 approved by the Secretary of Commerce.
Other interesting functions output a bounded size digital footprint (checksum) of a file (like md5). This is very useful
for checking data integrity of downloads over the internet. The md5 hash is a bit number.
Instead of listing or bits for the hash value one uses hexadecimal notation with digits
in 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , a, b, c, d, e, f. A pair of hexadecimal digits then represents
a byte or bits. Output from sha-256 and md5 consist of and hexadecimal
digits respectively. You are welcome to experiment with these two hash functions in the
Sage window below.
What is the sha-256 hash of your name? Change a
few letters and recompute. Do you see any system? What about the md5 hash function?
Can you find two different strings with the same md5 hash using your computer?
I have not answered the last question myself, but I am told that it is possible to find
a collision for md5 using a garden variety home computer. Browsing the internet, it
seems that the two strings and given in
hexadecimal notation
This notation represents a sequence of bytes given by pairs of hexadecimal digits
by
d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f89
55ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5b
d8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70
d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f89
55ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5b
d8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0
e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70
1.9.1 When are two functions the same?
The functions and
given by and are not the same! Their domains
are different.
1.9.2 Notations for defining a function
What is and for the function defined in
(1.19)
. Draw
the graph of . Come up with a function , where it
does not make sense to draw a graph.
1.9.3 Composition of functions
The concept of a function is powerful and underlies functional programming in computer science: every computation can be realized as applying a composition of functions to an argument. This is exemplified in the computer language
Haskell.
Suppose that
and that and are given by the tables
Compute the table for . Show that is not
injective. Adjust the table for so that becomes bijective.
Consider and given by
What is as a function from to in terms of ?
1.9.4 Functions from and into products
Suppose that
as in
(1.13)
. Then the function
given by
is called the projection on the -th coordinate.
If is a function, then
where .
Suppose that and . Then
Now suppose that and that is given by
Then
1.9.5 Injective and surjective functions
Let be a function. Then is called
- injective, if for every .
- surjective, if for every , there exists , such that .
- bijective, if it is both injective and surjective.
Is a cryptographic hash-function as defined in Example
1.92
injective?
Suppose that
and that the function is defined by the table
Is injective? Is it surjective? Is it possible to adjust the table so that
becomes injective?
Is it possible to adjust the table so that
becomes surjective?
Consider the function given by
where .
Is injective? Is surjective? Suggest how to change and so that becomes
bijective.
Consider the function given by
Show that is bijective.
Write down precisely how the truth table for may
be expressed in terms of a function . What are the sets and in this case?
1.9.6 The inverse function
Let , where be given by
the table
Then is given by the table
What if the definition of in Example
1.107
is changed to
Does make sense here?
What is the inverse function of given by ?
What is the inverse function of , where and
?
1.9.7 The preimage
Consider a
function
where and are sets. If , then the
preimage of under is defined by
Consider the function , where and
given by
For , as illustrated below.
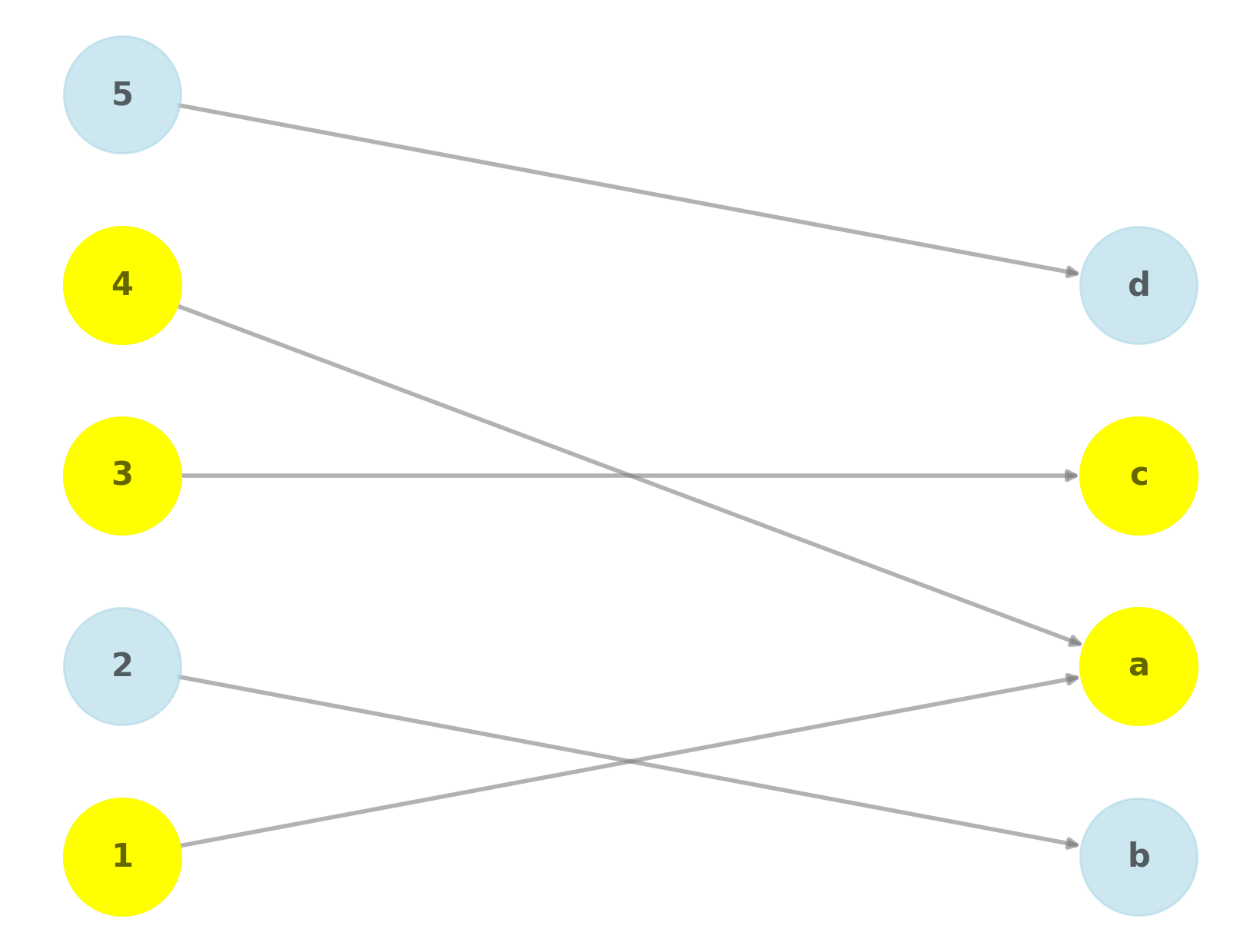

What is when and
?
Consider the function given by
and let . What is true about ?
1.9.8 Neural networks
Consider the three perceptrons , where
and
Let . Then is
a composite function of two functions
and . Write down these functions.
Hint
Compute
and .
Relate the perceptrons and to the illustration
below. What do you think the red and blue line illustrate? What does
it mean that a dot is solid compared to hollow? What is special
about points between the red and blue lines? Try to relate and to the illustration.
\begin{excluderag}
 (Illustration courtesy of William Heyman Krill).
\end{excluderag}
(Illustration courtesy of William Heyman Krill).
\end{excluderag}
Have a closer look at
(1.22)
in order to understand how
functions from to are expressed. Notice that
our notation is a bit inconsistent when it comes to types. For example,
the function should really be
denoted instead of , since it takes input from
. This is remedied in the (hopefully easy to understand) python code below.
LLM
💬
Explain the python code below to me.
def p1(v):
(x, y) = v
if -x-y > -3/2:
return 1
else:
return 0
def p2(v):
(x, y) = v
if x + y > 1/2:
return 1
else:
return 0
def p3(v):
(x, y) = v
if x+y > 3/2:
return 1
else:
return 0
def h(v):
return (p1(v), p2(v))
def g(v):
return p3(v)
def f(v):
return g(h(v))
Give weights and a threshold for a perceptron that computes
the logical and function i.e, must satisfy
Do the same for the logical or function .
Is it possible to find a perceptron , such that
What if you are allowed to use a neural network composed as (one hidden layer)
 ?
?