5Euclidean vector spaces

Big data are made up of many numbers in data sets. Such data sets can be represented as vectors in a high dimensional euclidean vector space. A vector is nothing but a list of numbers, but we need to talk mathematically about the size of a vector and perform operations on vectors. The term euclidean refers to vectors with a dot product as known from the plane $\mathbb{R}^2$ .

The purpose of this chapter is to set the stage for this, especially by introducing the dot product (or inner product) for general vectors. Having a dot product is immensely useful and we give several applications like linear regression and the perceptron learning algorithm

In the last part of the chapter we will list rudimentary basics of analysis starting with bounded, open, closed and compact subsets of euclidean spaces leading to continuous functions and the socalled extreme value theorem, Theorem 5.66 . This result states that a huge class of optimization problems always have a solution.

5.1 Vectors in the plane

The dot product (or inner product) between two vectors $u, v\in \mathbb{R}^2$ is given by

$u\cdot v = x_1 x_2 + y_1 y_2, \tag{5.1}$ where

$u = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}\qquad\text{and}\qquad v = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}. \tag{5.2}$ We may also interpret $u$ and $v$ as $2\times 1$ matrices (or column vectors). Then the dot product in (5.1) may be realized as the matrix product:

$u\cdot v = u^\intercal v.$ The length or norm of the vector $u\in \mathbb{R}^2$ is given by

$\left\vert u \right\vert = \sqrt{u\cdot u} = \sqrt{u^\intercal u} = \sqrt{x_1^2 + y_1^2}.$ This follows from the Pythagorean theorem:

The distance $d(u, v)$ between the two vectors $u$ and $v$ is given by

$d(u, v) = |u-v| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$ Also, the cosine of the angle $\theta$ between $u$ and $v$ is given by

$\cos(\theta) = \frac{u\cdot v}{\left\vert u \right\vert\left\vert v \right\vert}\qquad\text{or}\qquad u \cdot v = \left\vert u \right\vert \left\vert v \right\vert \cos(\theta).$ We will not go into this formula. It is a byproduct of considering the projection of a vector on another vector (see Exercise 5.6 ).

All of these rather natural notions in the plane $\mathbb{R}^2$ generalize naturally to $\mathbb{R}^n$ for $n>2$ .

5.2 Higher dimensions

We denote the set of column vectors with $n$ rows by $\mathbb{R}^n$ and call it the euclidean vector space of dimension $n$ . An element $v\in \mathbb{R}^n$ is called a vector and it has the form (column vector with $d$ entries)

$v = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}.$

A vector in $\mathbb{R}^n$ is a model for a data set in real life. A collection of $d$ numbers, which could signify $d$ measurements. You will see an example of this below, where a vector represents a data set counting words in a string.

Being column vectors, vectors in $\mathbb{R}^n$ can be added and multiplied by numbers:

$\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} + \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} = \begin{pmatrix} x_1 + y_1 \\ x_2 + y_2\\ \vdots \\ x_n + y_n \end{pmatrix}\qquad\qquad \lambda \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} \lambda x_1 \\ \lambda x_2 \\ \vdots \\ \lambda x_n \end{pmatrix}.$

The dot product generalizes as follows to higher dimensions.

5.2.1 Dot product, norm and cosine

Suppose that

$u = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\qquad \text{and} \qquad v = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}$ are vectors in $\mathbb{R}^n$ .

The dot product between $u$ and $v$ is defined by
$u\cdot v = u^\top v = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n. \tag{5.3}$
Two vectors $u, v\in \mathbb{R}^n$ are called orthogonal if $u\cdot v = 0$ . We write this as $u \perp v$ .
The norm of $u\in \mathbb{R}^n$ is defined by
$\left\vert u \right\vert = \sqrt{u\cdot u} = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}. \tag{5.4}$
The distance between the two vectors $u$ and $v$ is defined by
$d(u, v) = | u - v | = \sqrt{(x_1-y_1)^2 + \cdots + (x_n - y_n)^2}.$
The cosine of the angle between $u$ and $v$ is defined by
$\frac{u\cdot v}{|u| |v|}$ provided that they both are non-zero.

All of the definitions above are present in modern machine learning frameworks. Below we see their incarnations in the python library numpy.

Show that

$u \perp u \iff u = 0,$ where $u\in \mathbb{R}^n$ .

Use the definition in (5.3) to show that

$\begin{aligned} u\cdot (v + w) &= u\cdot v + u\cdot w\\ (\lambda u)\cdot v &= u\cdot (\lambda v) = \lambda (u\cdot v) \end{aligned}$ for $u, v, w\in \mathbb{R}^n$ and $\lambda\in\mathbb{R}$ .

Let $u\in \mathbb{R}^n$ be a nonzero vector and $\lambda\in \mathbb{R}$ . Use the definition in (5.4) to show that $|\lambda u| = |\lambda| \, |u|$ and that

$\frac{1}{|u|} u$ is a unit vector.

You could perhaps use Exercise 5.4 to do this. Notice also that $|\lambda|$ is the absolute value for $\lambda$ if $\lambda\in \mathbb{R}$ .

Given two vectors $u, v\in \mathbb{R}^n$ with $v\neq 0$ , find $\lambda\in \mathbb{R}$ , such that $u - \lambda v$ and $v$ are orthogonal, i.e.

$(u - \lambda v) \cdot v = 0.$

$(u - \lambda v) \cdot v = 0 \iff (u\cdot v) - \lambda (v\cdot v) = 0.$ This is an equation, where $\lambda$ is unknown!

For $d=2$ , it is sketched below that if $u - \lambda v$ and $v$ are orthogonal, then $u, \lambda v$ and $u-\lambda v$ are the sides in a right triangle.

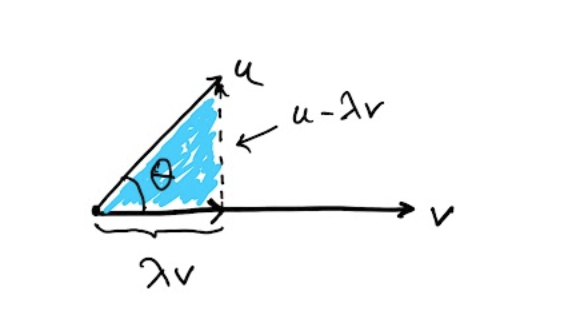In this case, if $\theta$ is the angle between $u$ and $v$ , show that

$\left\vert u \right\vert \cos(\theta) = \left\vert v \right\vert \lambda.$ Use this to show that

$u\cdot v = \left\vert u \right\vert \left\vert v \right\vert \cos(\theta).$ Finally show that

$\cos(A - B) = \cos(A) \cos(B) + \sin(A) \sin(B),$ where $A$ and $B$ are two angles.

In the last question, you could use that the vectors

$\begin{pmatrix} \cos(A)\\ \sin(A) \end{pmatrix}\qquad\text{and}\qquad \begin{pmatrix} \cos(B)\\ \sin(B) \end{pmatrix}$ are unit vectors.

Given two vectors $u, v\in \mathbb{R}^n$ , solve the minimization problem

$\begin{aligned} &\text{Minimize} &\left\vert u - \lambda v \right\vert&\\ &\text{with constraint}\\ &&\lambda\in\mathbb{R}. \end{aligned}$

First convince yourself that $\lambda$ minimizes $\left\vert u - \lambda v \right\vert$ if and only if it minimizes

$(u - \lambda v)\cdot (u - \lambda v) = \left\vert v \right\vert^2 \lambda^2 - 2 (u\cdot v)\lambda + \left\vert u \right\vert^2,$ which happens to be a quadratic polynomial in $\lambda$ .

5.3 The unreasonable effectiveness of the dot product

Let $d$ denote the distance from $(1, 1)$ to the line through $(0, 0)$ and $(2, 1)$ . What is true about $d$ ?

$d = \frac{1}{2}.$

$d = 0.447214.$

$d = \frac{\sqrt{5}}{5}.$

$d = \frac{2}{\sqrt{5}}.$

5.3.1 The dist formula from high school

The infamous dist formula from high school says that the distance from the point $(x_1, y_1)$ to the line given by $y = a x + b$ is

$\frac{\left\vert a x_1 + b - y_1 \right\vert}{\sqrt{a^2 + 1}}. \tag{5.5}$ Where does this magical formula come from? Consider a general line $L$ in parametrized form (see Definition 4.10 )

$L = \{ u + t v\mid t\in \mathbb{R}\} \subseteq \mathbb{R}^n.$ If $w\in \mathbb{R}^n$ , then the distance from $w$ to $L$ is given by the solution $t_0$ to the optimization problem

$\begin{aligned} &\text{min}\, (w - (u + t v))\cdot (w - (u + t v))\\ &t\in \mathbb{R}. \end{aligned}\tag{5.6}$ This looks scary, but simply boils down to finding the top of a parabola. The solution is

$t_0 = \frac{v\cdot w - u\cdot v}{v\cdot v}$ and the point on $L$ closest to $w$ is $u + t_0 v$ .

Now we put (see Example 4.11 )

$u = \begin{pmatrix} 0 \\ b \end{pmatrix}, \quad v = \begin{pmatrix} 1 \\ a \end{pmatrix}\quad\text{and}\quad w = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}$ in order to derive (5.5) . The solution to (5.6) becomes

$t_0 = \frac{x_1 + a y_1 - a b}{1 + a^2}.$ We must compute the distance $D$ from $w$ to $u + t_0 v$ in this case. The distance squared is

$\begin{aligned} D^2 &= |w - (u + t_0 v)|^2 = (w - (u + t_0 v))\cdot (w - (u + t_0 v)) \\ &=(x_1 - t_0)^2 + (y_1 - b - t_0 a)^2. \end{aligned}$ This is a mouthful and I have to admit that I used symbolic software (see below) to verify that

$D^2 = \frac{a^2 x_1^2 + 2 a b x_1 - 2 a x_1 y_1 + b^2 - 2 b y_1 + y_1^2}{1 + a^2} = \frac{(a x_1 + b - y_1)^2}{1+a^2}.$

5.3.2 The perceptron algorithm

Already at this point we have the necessary definitions for explaining the perceptron algorithm. This is one of the early algorithms of machine learning. It aims at finding a high dimensional line (hyperplane) that separates data organized in two clusters. In terms of the dot product, the idea of the algorithm is described below in dimension two.

A line in the plane is given by an equation

$a x + b y + c = 0$ for $a, b, c\in \mathbb{R}$ , where $(a, b) \neq (0,0)$ . Given finitely many points

$v_1 = (x_1, y_1), v_2 = (x_2, y_2), \dots, v_n = (x_n, y_n)$ each with a label $\ell_1, \dots, \ell_n$ of $\pm 1$ (or blue and red for that matter), we wish to find a line (given by $a, b, c$ ), such that

$\begin{aligned} a x_i + b y_i + c &> 0\quad\text{if}\quad \ell_i = 1\\ a x_i + b y_i + c &< 0\quad\text{if}\quad \ell_i = -1 \end{aligned}$ for $i = 1, \dots, n$ . Such a line is called a separating line for the labeled points.

In some cases this is impossible (an example is illustrated below).

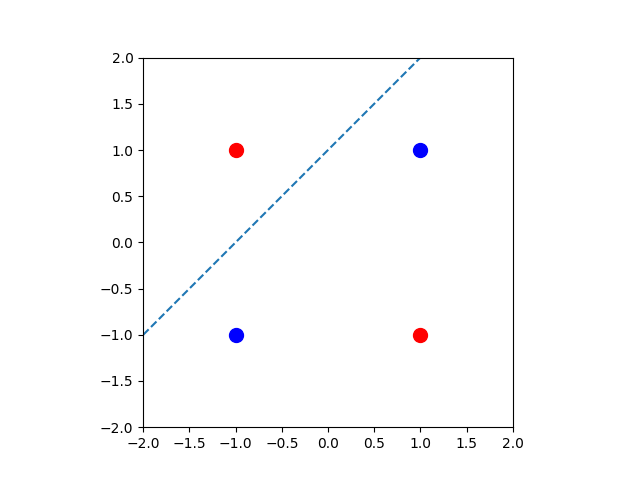
Show that it is imposible to find a line separating the red and blue points above. The red points are $(-1, 1)$ and $(1, -1)$ . The blue points are $(-1, -1)$ and $(1, 1)$ .

A clever approach to finding such a line, if it exists, is to reformulate the problem by looking at the vectors given by

$\hat{v}_1 = (\ell_1 x_1, \ell_1 y_1, \ell_1),\qquad \hat{v}_2 = (\ell _2 x_2, \ell_2 y_2, \ell_2),\qquad \dots\qquad ,\qquad \hat{v}_n = (\ell_n x_n, \ell_n y_n, \ell_n) \tag{5.7}$ in $\mathbb{R}^3$ . Then the existence of the line is equivalent to the existence of a vector $\alpha\in \mathbb{R}^3$ with $\alpha \cdot \hat{v}_i > 0$ for $i = 1, \dots, n$ . If $\alpha = (\alpha_1, \alpha_2, \alpha_3)$ is such a vector, then we have for $i = 1, \dots, n$ ,

$\begin{aligned} \alpha_1 x_i + \alpha_2 y_i + \alpha_3 &> 0\quad\text{if}\quad \ell_i = 1\\ -\alpha_1 x_i - \alpha_2 y_i - \alpha_3 &> 0\quad\text{if}\quad \ell_i = -1. \end{aligned}\tag{5.8}$ Therefore we may take $a = \alpha_1, b = \alpha_2$ and $c = \alpha_3$ as the line.

A ridiculously simple algorithm

In view of the approach introduced in (5.8) , the the following general question is interesting.

Given finitely many vectors $v_1, \dots, v_m\in \mathbb{R}^n\setminus\{0\}$ , can we find $\alpha\in \mathbb{R}^n$ , such that

$\alpha\cdot v_i > 0$ for every $i = 1, \dots, m$ ?

Come up with a simple example, where this problem is unsolvable i.e., come up with vectors $v_1, \dots, v_n\in \mathbb{R}^n$ , where such an $\alpha$ does not exist.

Hint

Try out some simple examples for $d=1$ and $d=2$ .

In case $\alpha$ exists, the following ridiculously simple algorithm works in computing $\alpha$ . It is called the perceptron (learning) algorithm.

Begin by putting $\alpha = 0$ .
If there exists $v_i\in \{v_1, \dots, v_m\}$ with $\alpha\cdot v_i \leq 0$ , then replace $\alpha$ by $\alpha + v_i$ and repeat this step. Otherwise $\alpha$ is the desired output vector.

Let us try out the algorithm on the simple example of just two points in $\mathbb{R}^2$ given by

$v_1 = \begin{pmatrix} -1 \\ \hphantom{-} 1 \end{pmatrix}\qquad\text{and}\qquad v_2 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}.$

In this case the algorithm proceeds as pictured below.

$\alpha = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\xrightarrow{+v_1} \begin{pmatrix} -1 \\ \hphantom{-} 1 \end{pmatrix} \xrightarrow{+v_2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \xrightarrow{+v_2}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \xrightarrow{+v_1}\begin{pmatrix} 0 \\ 2 \end{pmatrix} \xrightarrow{+v_2} \begin{pmatrix} 1 \\ 2 \end{pmatrix}.$

It patiently crawls its way ending with the vector $\alpha = \begin{pmatrix} 1 \\ 2 \end{pmatrix}$ , which satisfies $\alpha\cdot v_1 > 0$ and $\alpha\cdot v_2 > 0$ .

Let us see how (5.7) works in a concrete example.

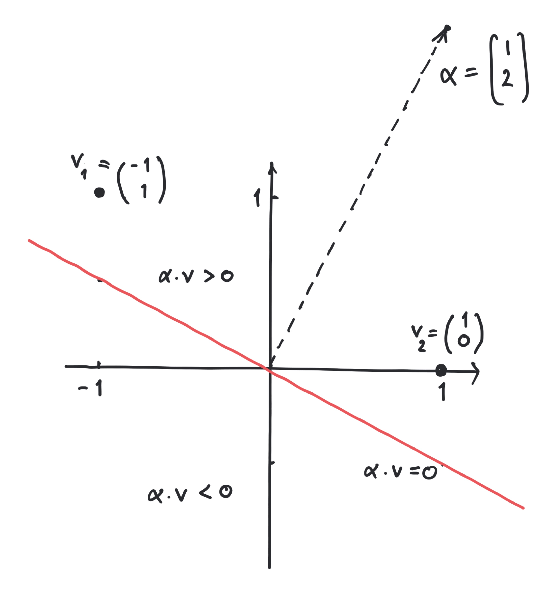
Consider the points

$v_1 = \begin{pmatrix} 0 \\ 0 \end{pmatrix},\qquad v_2=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\qquad\text{and}\qquad v_3=\begin{pmatrix} \hphantom{-} 1 \\ -1 \end{pmatrix}$ in $\mathbb{R}^2$ , where $v_1$ and $v_2$ are labeled by $+1$ and $v_3$ is labeled by $-1$ . Then we let

$\hat{v}_1 = \begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix},\qquad \hat{v}_2 = \begin{pmatrix} 1 \\ 1 \\ 1\end{pmatrix}\qquad \text{and}\qquad \hat{v}_3 = \begin{pmatrix} -1 \\ \hphantom{-} 1 \\ -1\end{pmatrix}.$ Now we run the simple algorithm above Example 5.11 :

$\hat{\alpha} = \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}\xrightarrow{+\hat{v}_1} \begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix} \xrightarrow{+\hat{v}_3} \begin{pmatrix} -1 \\ \hphantom{-} 1 \\ \hphantom{-} 0\end{pmatrix} \xrightarrow{+\hat{v}_1} \begin{pmatrix} - 1 \\ \hphantom{-} 1 \\ \hphantom{-} 1\end{pmatrix}.$

From the last vector we see that $x - y - 1 = 0$ determines a line separating the labeled points.

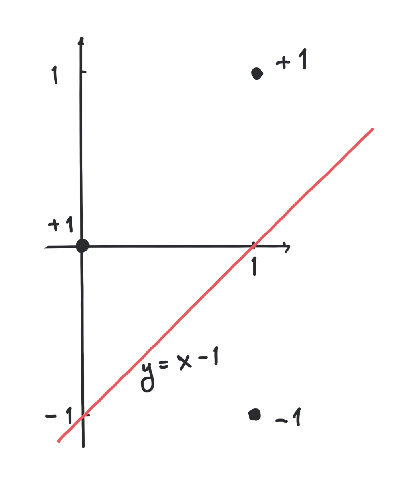
Below is an implementation of the perceptron (learning) algorithm in python (with numpy) with input from Example 5.12 (it also works in higher dimensions).

Consider the points

$\begin{pmatrix} 0 \\ 0 \end{pmatrix},\qquad \begin{pmatrix} 0 \\ 1 \end{pmatrix},\qquad \begin{pmatrix} 1 \\ 1 \end{pmatrix},\qquad\text{and}\qquad \begin{pmatrix} 1 \\ 0 \end{pmatrix}$ in $\mathbb{R}^2$ , where the first point is labeled with $-1$ and the rest by $1$ . Use the perceptron algorithm to compute a separating hyperplane.

What happens when you run the perceptron algorithm on the above points, but where the label of

$\begin{pmatrix} 1 \\ 1 \end{pmatrix}$ is changed from $1$ to $-1$ ?

5.3.3 Why does the perceptron algorithm work?

We will assume that there exists $\alpha\in \mathbb{R}^n$ , such that

$\alpha\cdot v_i > 0$ for every $i = 1, \dots, m$ . Therefore $\mu = \min(\alpha\cdot v_1, \dots, \alpha\cdot v_m) > 0$ and if we put

$\alpha^* = \frac{1}{\mu} \alpha, \tag{5.9}$ then $\alpha^*\cdot v_i \geq 1$ for every $i = 1, \dots, m$ .

The basic insight is the following

Let $r = \max\{\left\vert v_1 \right\vert, \dots, \left\vert v_m \right\vert\}$ . After $k$ iterations of the perceptron algorithm, $\alpha$ satisfies

$\alpha\cdot \alpha^* \geq k \qquad\text{and}\qquad k r^2 \geq \left\vert \alpha \right\vert^2,$ where $\alpha^*$ is defined in (5.9) .

The algorithm starts with $\alpha = 0$ . In the second step we update $\alpha$ to $\alpha + v_i$ if $\alpha\cdot v_i \leq 0$ . For such a $v_i$ we have the following inequalities

$(\alpha + v_i)\cdot \alpha^* = \alpha\cdot \alpha^* + v_i\cdot \alpha^* \geq \alpha\cdot \alpha^* + 1$ and

$(\alpha + v_i)\cdot (\alpha + v_i) = \left\vert \alpha \right\vert^2 + 2 v_i\cdot \alpha + \left\vert v_i \right\vert^2 \leq \left\vert \alpha \right\vert^2 + \left\vert v_i \right\vert^2 \leq \left\vert \alpha \right\vert^2 + r^2.$ If the second step of the algorithm is executed after $k$ steps, then we get for the new $\alpha + v_i$ that

$(\alpha + v_i)\cdot \alpha^* \geq \alpha \cdot \alpha^* + 1 \geq k + 1\qquad\text{and}\qquad |\alpha + v_i|^2 \leq |\alpha|^2 + r^2 \leq k r^2 + r^2 = (k+1) r^2.$

Proposition 5.14 implies that

$k \leq \left\vert \alpha \right\vert \left\vert \alpha^* \right\vert \leq \sqrt{k} r \left\vert \alpha^* \right\vert.$ Therefore we get $k\leq r^2 \left\vert \alpha^* \right\vert^2$ and there is an upper bound on the number of iterations used in the second step. So after a finite number of steps, we must have $\alpha \cdot v_i > 0$ for every $i = 1, \dots, m$ .

5.4 Pythagoras and the least squares method

The result below is a generalization of the theorem of Pythagoras about right triangles to higher dimensions.

If $u, v\in \mathbb{R}^n$ and $u\perp v$ , then

$\left\vert u + v \right\vert^2 = \left\vert u \right\vert^2 + \left\vert v \right\vert^2.$

This follows from

$(u + v)\cdot(u+v) = u\cdot u + u\cdot v + v\cdot u + v\cdot v = u\cdot u + v\cdot v = \left\vert u \right\vert^2 + \left\vert v \right\vert^2,$ since $u \cdot v = v\cdot u = 0$ .

The dot product and the norm have a vast number of applications. One of them is the method of least squares: suppose that you are presented with a system

$A x = b \tag{5.10}$ of linear equations, where $A$ is an $m\times n$ matrix.

You may not be able to solve (5.10) . There could be for example $17$ equations and only $2$ unknowns making it impossible for all the equations to hold. As an example, the system

$\begin{pmatrix} \phantom{-} 1 & \phantom{-} 1\\ \phantom{-} 1 & -1\\ -1 & \phantom{-} 1 \end{pmatrix} \begin{pmatrix} x \\ y\end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 1 \end{pmatrix} \tag{5.11}$ of three linear equations and two unknowns does not have any solutions.

The method of (linear) least squares seeks the best approximate solution $x_0$ to (5.10) as a solution to the minimization problem

$\begin{aligned} &\text{Minimize} &\left\vert b - A x \right\vert^2&\\ &\text{with constraint}\\ &&x\in\mathbb{R}^n. \end{aligned}\tag{5.12}$

There is a surprising way of finding optimal solutions to (5.12) :

If $x_0\in\mathbb{R}^n$ is a solution to the system

$(A^\top A) x = A^\top b \tag{5.13}$ of $n$ linear equations with $n$ unknowns, then $x_0$ is an optimal solution to (5.12) . If $x_0$ on the other hand is an optimal solution to (5.12) , then $x_0$ is a solution to (5.13) .

Suppose we know that $b - A x_0$ is orthogonal to $A v$ for every $v\in \mathbb{R}^n$ . Then

$\left\vert b - A x \right\vert^2 = \left\vert b - A x_0 + A(x_0 - x) \right\vert^2 = \left\vert b - A x_0 \right\vert^2 + \left\vert A(x-x_0) \right\vert^2$ for every $x\in \mathbb{R}^n$ by Proposition 5.15 . So, in the case that $b - A x_0 \perp A v$ for every $v\in \mathbb{R}^n$ we have

$\left\vert b - A x \right\vert^2 \geq \left\vert b - A x_0 \right\vert^2$ for every $x\in \mathbb{R}^n$ proving that $x_0$ is an optimal solution to (5.12) .

Now we wish to show that $b - A x_0$ is orthogonal to $A v$ for every $v\in \mathbb{R}^n$ if and only if $A^\top A x_0 = A^\top b$ . This is a computation involving the matrix arithmetic introduced in Chapter 3 :

$\begin{aligned} &(b - A x_0)\cdot A v = \\ &(b - A x_0)^\top A v =\\ &b^\top A v - x_0^\top A^\top A v = \\ &(b^\top A - x_0^\top A^\top A) v = 0 \end{aligned}$ for every $v\in \mathbb{R}^n$ if and only if $b^\top A - x_0 A^\top A = 0$ . But

$(b^\top A - x_0^\top A^\top A)^\top = A^\top b - A^\top A x_0$ so that $(A^\top A) x_0 = A^\top b$ .

On the other hand, if $|b - A x_0|^2 \leq |b - A x|^2$ for every $x\in \mathbb{R}^n$ , then $(b - A x_0)\cdot A v = 0$ for every $v\in \mathbb{R}^n$ : if we could find $v$ with $(b - A x_0)\cdot A v < 0$ , then

$|b - A(x_0 - \epsilon v)|^2 <|b - A x_0|^2$ for a small number $\epsilon > 0$ . This follows, since

$|b - A(x_0 - \epsilon v)|^2 = ((b - A x_0) + \epsilon A v)^2,$ which is

$|b - A x_0|^2 + 2\epsilon (b - A x_0)\cdot A v + \epsilon^2 (A v)^2$ By picking $\epsilon>0$ sufficiently small,

$\epsilon (2(b-A x_0)\cdot A v + \epsilon (A v)^2) < 0.$

In a future course on linear algebra you will see that the system of linear equations in Theorem 5.16 is always solvable i.e., an optimal solution to (5.12) can always be found in this way.

Show that (5.11) has no solutions. Compute the best approximate solution to (5.11) using Theorem 5.16 .

The classical application of the least squares method is to find the best line $y = \alpha x + \beta$ through a given set of points

$(x_1, y_1), \quad (x_2, y_2), \quad \dots \quad, (x_n, y_n)$ in the plane $\mathbb{R}^2$ .

Usually we cannot find a line matching the points precisely. This corresponds to the fact that the system of equations

$\begin{pmatrix} x_1 & 1\\ x_2 & 1\\ \vdots & \vdots\\ x_n & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}$ has no solutions.

Working with the least squares solution, we try to compute the best line $y = \alpha x + \beta$ in the sense that

$(y_1 -\alpha x_1 -\beta)^2 + (y_2 -\alpha x_2 -\beta)^2 + \cdots + (y_n -\alpha x_n -\beta)^2$ is minimized.

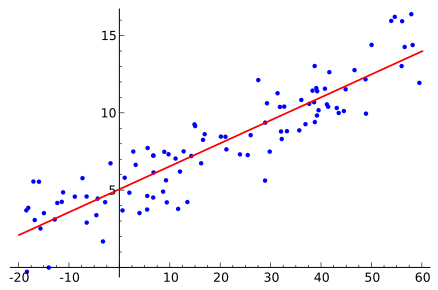
Best fit of line to random points from Wikipedia.

We might as well have asked for the best quadratic polynomial

$y = \alpha x^2 + \beta x + \gamma$ passing through the points

$(x_1, y_1), \quad (x_2, y_2), \quad \dots \quad, (x_n, y_n)$ in $\mathbb{R}^2$ .

The same method gives us the system

$\begin{pmatrix} x_1^2 & x_1 & 1\\ x_2 ^2 & x_2 & 1\\ \vdots & \vdots\\ x_n^2 & x_n & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \\ \gamma \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}$ of linear equations.

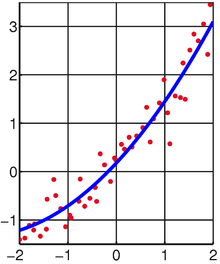
Best fit of quadratic polynomial to random points from Wikipedia.

The method generalizes naturally to finding the best polynomial of degree $m$

$y = a_m x^m + a_{m-1} x^{m-1} + \cdots + a_1 x + a_0$ through a given set of points.

Find the best line $y = \alpha x + \beta$ through the points $(1, 2), (2,1)$ and $(4,3)$ and the best quadratic polynomial $y = a x^2 + b x + c$ through the points $(-2, 2), (-1, 1), (0,0), (1,1)$ and $(2,2)$ .

It is important here, that you write down the relevant system of linear equations according to Theorem 5.16 . It is however ok to solve the equations on a computer (or check your best fit on WolframAlpha).

Also, you can get a graphical illustration of your result in the sage window below.

A circle with center $(a, b)$ and radius $r$ is given by the equation

$(x - a)^2 + (y - b)^2 = r^2. \tag{5.14}$

Explain how (5.14) can be rewritten to the equation
$2 a x + 2 b y + c = x^2 + y^2, \tag{5.15}$ where $c = r^2 - a^2 - b^2$ .
Explain how fitting a circle to the points $(x_1, y_1), \dots, (x_n, y_n)$ in the least squares context using (5.15) leads to the system
$\begin{pmatrix} 2 x_1 & 2 y_1 & 1\\ 2 x_2 & 2 y_2 & 1\\ \vdots &\vdots &\vdots\\ 2 x_n & 2 y_n & 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} x_1^2 + y_1^2\\ x_2^2 + y_2^2\\ \vdots \\ x_n^2 + y_n^2 \end{pmatrix},$ of linear equations.
Compute the best circle through the points
$(0, 2),\quad (0, 3),\quad (2,0)\quad\text{and}\quad (3, 1)$ by giving the center coordinates and radius with two decimals. Use the Sage window below to plot your result too see if it matches the drawing.

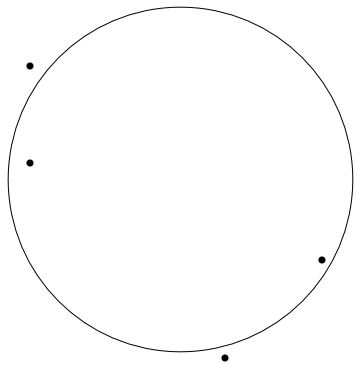
5.5 The Cauchy-Schwarz inequality

Take another look at (5) in Definition 5.1 . It is actually a small miracle that no matter which (non-zero) vectors $u$ and $v$ you use as input to the cosine function defined in Example 5.2 , you always get a number between $-1$ and $1$ . The mathematics behind this is rather elegant. It is a consequence of the famous Cauchy-Schwarz inequality stated and proved below.

For two vectors $u, v\in \mathbb{R}^n$ ,

$\left\vert u\cdot v \right\vert \leq \left\vert u \right\vert \left\vert v \right\vert.$

We consider the function $q:\mathbb{R}\rightarrow \mathbb{R}$ given by

$q(x) = (x u + v)\cdot (x u + v) = \left\vert u \right\vert^2 x^2 + 2 (u\cdot v) x + \left\vert v \right\vert^2$ Then $q(x)$ is a quadratic polynomial with $q(x)\geq 0$ . Therefore its discriminant must be $\leq 0$ i.e.,

$4 (u\cdot v)^2 - 4 \left\vert u \right\vert^2 \left\vert v \right\vert^2 \leq 0,$ which gives the result.

Why are the two inequalities

$-1 \leq \frac{u\cdot v}{ |u| |v| }\leq 1$ a consequence of Theorem 5.23 ?

For arbitrary two numbers $x, y\in \mathbb{R}$ ,

$2 (x^2 + y^2) \geq (x + y)^2,$ since

$2(x^2 + y^2) - (x + y)^2 = x^2 + y^2 - 2 x y = (x - y)^2\geq 0.$

Why is

$n (x_1^2 + \cdots + x_n^2) \geq (x_1 + \cdots + x_n)^2$ for arbitary $n$ numbers $x_1, \dots, x_n\in \mathbb{R}$ ?

5.5.1 The triangle inequality

Another nice consequence of the Cauchy-Schwarz inquality is the triangle inquality.

For three vectors $u, v, w\in \mathbb{R}^n$ ,

$d(u, w) \leq d(u, v) + d(v, w).$

From the Cauchy-Schwarz inequality (Theorem 5.23 ) it follows that

$\left\vert v_1+v_2 \right\vert^2 = (v_1+v_2)\cdot (v_1+v_2) = \left\vert v_1 \right\vert^2 + 2 v_1\cdot v_2 + \left\vert v_1 \right\vert^2 \leq \left\vert v_1 \right\vert^2 + 2 \left\vert v_1 \right\vert\left\vert v_2 \right\vert + \left\vert v_2 \right\vert^2$ for two vectors $v_1, v_2\in \mathbb{R}^n$ . Since the right hand side of this inequality is $(\left\vert v_1 \right\vert + \left\vert v_2 \right\vert)^2$ , we have

$\left\vert v_1 + v_2 \right\vert\leq \left\vert v_1 \right\vert + \left\vert v_2 \right\vert.$ By the definition of $d(u, w)$ , we then get the desired inequality as

$d(u, w) = |u-w| = | (u-v) + (v-w)| \leq |u-v| + |v-w| = d(u, v) + d(v, w).$

Apply the triangly inequality in the form

$|u + v| \leq |u| + |v|$ for $u, v\in \mathbb{R}^n$ to show that

$\begin{aligned} \left\vert \left\vert u \right\vert-\left\vert v \right\vert \right\vert &\leq \left\vert u - v \right\vert\\ \left\vert \left\vert u \right\vert-\left\vert v \right\vert \right\vert &\leq \left\vert u + v \right\vert. \end{aligned}$

5.5.2 Cosine similarity in machine learning

When vectors two vectors $u, v\in \mathbb{R}^n$ are interpreted as data sets, the number in (5) of Definition 5.1 is known as the cosine similarity. It measures the correlation between the vectors $u$ and $v$ .

A very primitive way of modelling sentences in a language is the socalled one-hot encoding of its words. We will illustrate this by an example. Suppose that our language consists of the words

'a', 'and', 'applicable', 'are', 'fun', 'is', 'mathematics', 'matrices', 'matrix', 'useful'

' Each word gets embedded into $\mathbb{R}^{10}$ with a vector associated to its row below

$\begin{array}{lll} \text{a} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[0.5em] \text{and} & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[0.5em] \text{applicable} & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[0.5em] \text{are} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\[0.5em] \text{fun} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\[0.5em] \text{is} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\[0.5em] \text{mathematics} & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\[0.5em] \text{matrices} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\[0.5em] \text{matrix} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\[0.5em] \text{useful}& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \tag{5.16}$

Now onsider the two sentences "mathematics is fun and a matrix is useful" and "mathematics is fun and matrices are applicable".

From the words in the two strings we form the following vectors in $\mathbb{R}^{10}$ using the one-hot embedding in (5.16) .

$\begin{array}{lll} \text{mathematics is fun and a matrix is useful} & 1 & 1 & 0 & 0 & 1 & 2 & 1 & 0 & 1 & 0\\[0.5em] \text{mathematics is fun and matrices are applicable} & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0\\[0.5em] \end{array}$

Here a sentence is mapped to the vector, which is the sum of all the vectors corresponding to the words in the sentence, where each vector is multiplied by its multiplicity i.e., how many times the word occurs. The closer the cosine gets to $1$ (corresponding to an angle of $0$ degrees), the more similar we consider the sentences. Use the python snippet below to experiment and compute the cosine similarity in the example.

Cosine similarity is crucial in machine learning, especially in NLP. The one-hot embedding is very crude and does not really capture the semantics of a sentence. The bread and butter of modern (large) language models is more advanced (dense) embeddings constructed using deep learning. The embeddings even take whole sentences as input! The recent breakthroughs can be traced back to 2013, where Google introduced the word embedding word2vec. When embedding a sentence one usually considers tokens and not words. This means that every sentence (as input to ChatGPT) must be broken down into a sequence of tokens. Modern large language models typically operate with around 50,000 tokens. Each token is embedded into a euclidean space of dimension usually $> 1000$ .

5.6 Special subsets of euclidean spaces

Recall that a circle (or an open disk) centered at $(x_0, y_0)\in \mathbb{R}^2$ with radius $r\in \mathbb{R}$ is defined as the subset

$\begin{aligned} &\left\{(x, y)\in \mathbb{R}^2 \middle| (x-x_0)^2 + (y - y_0)^2 < r^2\right\} =\\ &\left\{(x, y)\in \mathbb{R}^2 \middle| \sqrt{(x-x_0)^2 + (y - y_0)^2} < r\right\} =\\ &\left\{(x, y)\in \mathbb{R}^2 \middle| d((x_0, y_0), (x, y)) < r\right\}. \end{aligned}$

Similarly an open ball in $\mathbb{R}^3$ centered at $(x_0, y_0, z_0)\in \mathbb{R}^3$ with radius $r\in \mathbb{R}$ is defined as the subset

$\begin{aligned} &\left\{(x, y, z)\in \mathbb{R}^3 \middle| (x-x_0)^2 + (y - y_0)^2 + (z - z_0)^2 < r^2\right\} =\\ &\left\{(x, y, z)\in \mathbb{R}^3 \middle| \sqrt{(x-x_0)^2 + (y - y_0)^2 + (z - z_0)^2} < r\right\} =\\ &\left\{(x, y, z)\in \mathbb{R}^3 \middle| d((x_0, y_0, z_0), (x, y, z)) < r\right\}. \end{aligned}$

The natural generalization of this definition to higher dimensions is given below.

The open ball centered at $u\in \mathbb{R}^n$ with radius $r\in \mathbb{R}$ is defined as

$B(v, r) = \{v\in \mathbb{R}^n \mid d(u, v) < r\}.$

5.6.1 Bounded subsets

It makes sense to defined bounded subsets as subsets that can be contained in a large enough open ball centered at $0$ :

A subset $S \subseteq \mathbb{R}^n$ is called bounded if there exists $R\in \mathbb{R}$ , such that

$S \subseteq B(0, R).$

Written out Definition 5.29 says that

$|u| = \sqrt{x_1^2 + \cdots + x_n^2}\leq R$ for every $u = (x_1, \dots, x_n)\in S$ . Boundedness of $S$ is also equivalent to the following two conditions

There exists $R$ , such that
$x_1^2 + \cdots + x_n^2 \leq R$ for every $(x_1, \dots, x_n)\in S$ .
There exists $R$ , such that
$|x_i| \leq R$ for $i = 1, \dots, n$ and every $(x_1, \dots, x_n)\in S$ .

Every finite subset is bounded (why?). For $d = 1$ , Definition 5.29 simply says

$\exists R\in \mathbb{R}\, \forall x\in S: |x|\leq R$ This implies that an interval $S = [a, b]$ is bounded by putting $R = \max(|a|, |b|)$ in Definition 5.29 .

LLM

💬

I find the definition below quite hard to understand. It is about bounded subsets.
Please explain it to me patiently, give some examples and test me afterwards.
'''
A subset $S \subseteq \mathbb{R}^n$ is called bounded if there exists $R\in \mathbb{R}$, such that
$$
S \subseteq B(0, R),
$$
where $B(0, R) =  \{v\in \mathbb{R}^n \mid d(0, v) < R\}$ and $d$ is the euclidean distance function.
'''

Show precisely that the subset $\mathbb{N}$ of $\mathbb{R}$ is not bounded, whereas the subset $\{1, \frac{1}{2}, \frac{1}{3}, \dots\}$ is.

Sketch why

$S = \{(x, y) \mid x\geq 0, y\geq 0, x + y\leq 1\}\subseteq \mathbb{R}^2$ is bounded. Now use Fourier-Motzkin elimination to show the same without sketching.

5.6.2 Open, closed and compact subsets and boundaries and interiors of subsets

Open subsets

An open subset of $\mathbb{R}^n$ is a subset consisting of points, that are interior in the following sense:

A subset $U\subseteq \mathbb{R}^n$ is called open if for every $v\in U$ , there exists $\epsilon > 0$ , such that

$B(v, \epsilon) \subseteq U.$

Decide whether each of the subsets given below are open.

$\{1\}$
$\mathbb{R}^n$
$[0, 1]$
$(0, 1)$

Prove that an open ball given by $B(v, \varepsilon)\subseteq \mathbb{R}^n$ is an open subset.

Suppose that $u\in B(v, \varepsilon)$ . Define a suitable $\varepsilon'>0$ for $u\in B(v, \varepsilon)$ and use Corollary 5.26 to conclude that $B(u, \varepsilon')\subseteq B(v, \varepsilon)$ .

Show that a finite subset of $\mathbb{R}^n$ is never open.

We will need the result below.

If $U_1, \dots, U_m \subseteq \mathbb{R}^n$ are open subsets, then

$U_1 \cup \cdots \cup U_m\qquad\text{and}\qquad U_1 \cap \cdots \cap U_m$ are open subsets.

Closed subsets

A subset $F\subseteq \mathbb{R}^n$ is called closed if $\mathbb{R}^n\setminus F$ is open.

In analogy with Proposition 5.37 we have the result below.

If $F_1, \dots, F_m \subseteq \mathbb{R}^n$ are closed subsets, then

$F_1 \cup \cdots \cup F_m\quad\text{and}\quad F_1 \cap \cdots \cap F_m$ are closed subsets.

Decide whether each of the subsets given below are closed.

$\{1\}$
$\mathbb{R}^n$
$[0, 1]$
$[0, 1)$

Open intervals

The following subsets

$\begin{aligned} (a, \infty) &= \{x\in \mathbb{R} \mid a < x\}\\ (-\infty, a) &= \{x\in \mathbb{R} \mid x < a\}\\ (a, b) &= \{x\in \mathbb{R} \mid a < x < b\} \\ \end{aligned}$ are open subsets of $\mathbb{R}$ for every $a, b\in \mathbb{R}$ .

Let us prove that $(a, \infty)$ is an open subset of $\mathbb{R}$ . If $x\in (a, \infty)$ , then we let $\varepsilon = x-a$ . Suppose that $|y-x| < \varepsilon$ . If $y > x$ , then $y>a$ and $y\in (a, \infty)$ . If $y < x$ , then $x - y < \varepsilon = x - a$ and therefore $y > a$ and $y\in (a, \infty)$ . We have proved that $(a, \infty)$ is an open subset.

A similiar proof shows that $(-\infty, a)$ is an open subset. If $a < b$ , then

$(a, b) = (-\infty, b) \cap (a, \infty),$ which is an open subset by the above and Proposition 5.37 .

Closed intervals

We have a similar result for closed subsets.

The following subsets

$\begin{aligned} [a, b] &= \{x\in \mathbb{R} \mid a \leq x \leq b\} \\ [a, \infty) &= \{x\in \mathbb{R} \mid a \leq x\}\\ (-\infty, a] &= \{x\in \mathbb{R} \mid x \leq a\} \end{aligned}$ are closed subsets of $\mathbb{R}$ for every $a, b\in \mathbb{R}$ .

The proof follows from Definition 5.38 and Proposition 5.41 . For example,

$\mathbb{R} \setminus [a, \infty) = (-\infty, a).$

Compact subsets

We single out the following very important class of subsets

A subset $C\subseteq \mathbb{R}^n$ is called compact if it is bounded and closed.

The boundary of a subset

The boundary of a subset $S$ is informally the subset of points barely touching $S$ :

This is made precise in the following definition.

The boundary $\partial S$ of a subset $S\subseteq \mathbb{R}^n$ is defined as

$\partial S = \{v\in \mathbb{R}^n \mid \forall \epsilon > 0: B(v, \epsilon) \cap S\neq \emptyset\qquad\text{and}\qquad B(v, \epsilon) \cap (\mathbb{R}^n\setminus S) \neq \emptyset\}.$

What is the boundary of $[0, 1]$ ? What about $(0, 1)$ ?

The interior of a subset

The interior of a subset consists of the points, which are interior to the subset. More precisely

The interior of a subset $S\subseteq \mathbb{R}^n$ is defined by

$S^\circ = \{v\in S\mid \exists \epsilon > 0: B(v, \epsilon) \subseteq S\}.$

Let $S = [0, 1]\subseteq \mathbb{R}$ and $S\times \{1\} = \{(x, 1) \mid x\in S\} \subseteq \mathbb{R}^2$ . First make a sketch of these two subsets in $\mathbb{R}$ and $\mathbb{R}^2$ respectively. Then find $S^\circ$ and $(S\times \{1\})^\circ$ .

5.7 Continuous functions

A function $f: S\rightarrow T$ , where $S \subseteq \mathbb{R}^m$ and $T\subseteq \mathbb{R}^n$ is called continuous at $v\in S$ if for every $\epsilon > 0$ , there exists $\delta > 0$ , such that

$u\in B(v, \delta)\cap S \implies f(u)\in B(f(v), \epsilon).$ for every $u$ . Equivalently,

$\forall \epsilon > 0\, \exists \delta > 0\, \forall u\in S: d(u, v) < \delta \implies d(f(u), f(v)) < \epsilon. \tag{5.17}$ The function $f$ is called continuous if it is continuous at every $v\in S$ .

LLM

💬

I find the definition below quite challenging to understand. Please explain it to me
patiently with lots of examples. Test me in the end.
'''
A function $f:\rightarrow T$, where $S \subseteq \mathbb{R}^m$ and $T\subseteq \mathbb{R}^n$ is
called \emph{continuous at $v\in S$} if for every $\epsilon > 0$, there exists $\delta > 0$, such that
\begin{equation}
\forall \epsilon > 0\, \exists \delta > 0\, \forall u\in S: d(u, v) < \delta \implies d(f(u), f(v)) < \epsilon.
\end{equation}
'''

Definition 5.48 is the formal definition of a continuous function. It is short and sweet, but takes some time to assimilate.

The limit of a function at a point

The definition presented in (5.17) is admittedly a bit long. I will introduce some notation to make it easier. Assume that we have the same setup as in Definition 5.48 , but that we do not require that $v\in S$ . Then we use the notation

$\lim_{u\to v} f(u) = w$ to mean

$\forall \epsilon > 0\, \exists \delta > 0\, \forall u\in S: d(u, v) < \delta \implies d(f(u), w) < \epsilon$ and say that $f(u)$ has limit $w$ as $u$ approaches $v$ (inside $S$ ). Then (5.17) reads

$\lim_{u\to v} f(u) = f(v).$ Here is a little exercise to practice the notation: suppose that

$\frac{x^2 - 1}{x-1}.$ Then $f$ is a function defined on $S = \mathbb{R}\setminus\{1\}$ . What is $\lim_{x\to 1} f(x)$ ?

To get an understanding, you should study the mother of all examples of non-continuous functions given below:

$f(x) = \begin{cases} 0 &\text{if } x > 0\\ 1 &\text{if } x \leq 0 \end{cases}. \tag{5.18}$

This is a function from $S=\mathbb{R}$ to $T=\mathbb{R}$ . It is impossible to plot it without lifting the pencil or defining such a beast without using a bracket as in (5.18) .

Let me sketch how the formal Definition 5.48 kills any hope of (5.18) being continuous at $v=0$ . To prove this we must prove that the negation of the proposition in (5.17) is true. This reads

$\exists \epsilon > 0\, \forall \delta > 0\, \exists u\in S: d(u, 0) < \delta \land d(f(u), 1) \geq \epsilon$ for the function defined in (5.18) . You can verify that the above is true by setting $\epsilon = \frac{1}{2}$ and $u = \frac{\delta}{2}$ . For these values,

$d(u, 0) = \frac{\delta}{2} < \delta\qquad\text{and}\qquad d(f(u), 1) = d(0, 1) = 1 \geq \frac{1}{2}.$

Almost all functions we encounter will be continuous. The function $f$ above is an anomaly.

Let us stop briefly once more and see Definition 5.48 in action.

Let $S = T = \mathbb{R}$ in Definition 5.48 . We consider the two functions

$\begin{aligned} f(x) &= x\\ g(x) &= c, \end{aligned}$ where $c\in \mathbb{R}$ i.e., $f$ is the identity function and $g$ is a constant function given by the real number $c$ . Both of these functions are continuous. Let us see why.

For the function $f$ , (5.17) reads

$\forall \epsilon > 0 \exists \delta > 0 \forall y\in \mathbb{R}: d(y, x) < \delta \implies d(f(y), f(x)) = d(y, x) < \epsilon.$ This is certainly true if we pick $\delta = \epsilon$ .

For the function $g$ , (5.17) reads

$\forall \epsilon > 0 \exists \delta > 0 \forall y\in \mathbb{R}: d(y, x) < \delta \implies d(f(y), f(x)) = d(c, c) = 0 < \epsilon.$ Here $\delta > 0$ can be picked arbitrary, since $0 = d(c, c) < \epsilon$ is always true.

5.7.1 An elegant way of characterizing a continuous function

Recall the definition of the preimage from Definition 1.110 and the definition of an open subset from Definition 5.33 . The following characterization of continuous functions came rather late in the history of mathematics.

Let $f: \mathbb{R}^m\rightarrow \mathbb{R}^n$ be a function. Then $f$ is continuous if and only if $f^{-1}(U)$ is open in $\mathbb{R}^m$ for every open subset $U\subseteq \mathbb{R}^n$ .

Let $U\subseteq \mathbb{R}^n$ be an open subset. Assume first that $f$ is continuous. We wish to prove that $f^{-1}(U)$ is open. Pick $v\in f^{-1}(U)$ and $\epsilon>0$ so that $B(f(v), \epsilon) \subseteq U$ . Now use the continuity of $f$ to pick $\delta>0$ so that (5.17) is satisfied i.e.,

$u\in B(v, \delta) \implies f(u)\in B(f(v), \epsilon) \tag{5.19}$ Since $B(f(v), \epsilon) \subseteq U$ , (5.19) says that

$B(v, \delta) \subseteq U$ showing that $f^{-1}(U)$ is an open subset.

Now suppose that $f^{-1}(U)$ is open whenever $U\subseteq \mathbb{R}^n$ is open. For $v\in \mathbb{R}^m$ and $\epsilon > 0$ we put $V = B(f(v), \epsilon)$ . Since $V$ is an open subset, $f^{-1}(V)$ is open and $v\in f^{-1}(V)$ . So we may find $\delta > 0$ so that $B(v, \delta) \subseteq f^{-1}(V)$ . But this is exactly the statement that

$u \in B(v, \delta) \implies f(u) \in B(f(v), \epsilon)$ showing that $f$ is continuous.

The following result is often a very useful tool in showing that a subset is closed.

If $F\subseteq \mathbb{R}^n$ is a closed subset and $f: \mathbb{R}^m\rightarrow \mathbb{R}^n$ a continuous function, then the preimage

$f^{-1}(F) = \{v\in \mathbb{R}^m \mid f(v)\in F\}$ is a closed subset of $\mathbb{R}^m$ .

If $F\subseteq \mathbb{R}^n$ is closed, then $\mathbb{R}^n\setminus F$ is open. Therefore

$f^{-1}(\mathbb{R}^n\setminus F) = f^{-1}(\mathbb{R}^n) \setminus f^{-1}(F) = \mathbb{R}^m \setminus f^{-1}(F)$ is open by Proposition 5.50 . This implies that $f^{-1}(F)$ is closed.

Let us assume for now that $f:\mathbb{R}^2\rightarrow \mathbb{R}$ given by $f(x, y) = x^2 + y^2$ is continuous (see Exercise 5.58 ). Then Proposition 5.51 shows that the subset

$\begin{aligned} &\{(x, y)\in \mathbb{R}^2\mid x^2 + y^2 \geq 1\} = \\ &\{(x, y)\in \mathbb{R}^2\mid f(x, y) \geq 1\} = \\ &\{(x, y)\in \mathbb{R}^2\mid f(x, y) \in [1, \infty)\} = \\ &f^{-1}([1, \infty)) \end{aligned}$ of $\mathbb{R}^2$ is closed, since $[1, \infty)$ is a closed subset of $\mathbb{R}$ by Proposition 5.42 .

Show formally that the subset

$\{(x, y)\in \mathbb{R}^2\mid x^2 + y^2 > 1\}$ is an open subset of $\mathbb{R}^2$ .

5.7.2 Working with continuous functions

We give now three important results, which can be used in concrete situations to verify that a given function is continuous. They can be proved without too much hassle. The first result below basically follows from the definition of the norm of a vector (see (5.4) ).

The projection functions $\pi_i:\mathbb{R}^n\rightarrow \mathbb{R}$ defined in Definition 1.99 are continuous. In general a function $f:S\rightarrow T$ is continuous if and only if $\pi_j\circ f: S\rightarrow \mathbb{R}$ is continuous for every $j = 1, \dots, n$ , where $S\subseteq \mathbb{R}^m$ and $T\subseteq \mathbb{R}^n$ .

Lemma 5.54 shows for example that the functions $f(x, y) = x$ and $g(x, y) = y$ are continuous functions from $\mathbb{R}^2$ to $\mathbb{R}$ .

Consider the vector function $f: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ given by

$f(x, y) = \begin{pmatrix} x^2 + y^2 \\ \sin(x y) \end{pmatrix}$ as an example. To prove that $f$ is continuous, Lemma 5.54 tells us that it is enough to prove that its coordinate functions $f_1, f_2:\mathbb{R}^2\rightarrow \mathbb{R}$

$\begin{aligned} f_1(x, y) &= x^2 + y^2\\ f_2(x, y) &= \sin (x y) \end{aligned}$ are continuous.

Definition 5.48 also behaves nicely when continuous functions are composed. This is the content of the following

Suppose that $g: S\rightarrow T$ and $f: T\rightarrow R$ are continuous functions, where $S\subseteq \mathbb{R}^n, T\subseteq \mathbb{R}^e$ and $R\subseteq \mathbb{R}^f$ . Then the composition

$(f\circ g): S\rightarrow R$ is continuous.

To get continuous functions from functions already known to be continuous using arithmetic operations, the result below is useful.

Let $f, g: U\rightarrow \mathbb{R}$ be functions defined on a subset $U\subseteq \mathbb{R}^n$ . If $f$ and $g$ are continuous, then the functions

$\begin{aligned} (f + g): U\rightarrow \mathbb{R}\qquad\text{given by}\quad &(f + g)(x) = f(x) + g(x)\\ (f g): U\rightarrow \mathbb{R}\qquad\text{given by}\quad &(f g)(x) = f(x) g(x)\\ (f/g): V\rightarrow \mathbb{R}\qquad\text{given by}\quad &(f/g)(x) = f(x)/g(x) \end{aligned}$ are continuous functions, where $V = \{x\in U\mid g(x)\neq 0\}$ (the last function is defined only if $g(x)\neq 0$ ).

This result is a consequence of the definition of continuity and Proposition 5.56 .

Show in detail that the function $f: \mathbb{R}^2\rightarrow \mathbb{R}$ given by

$f(x, y) = x^2 + y^2$ is continuous by using Proposition 5.57 combined with Lemma 5.54 .

By combining Example 5.49 with Proposition 5.57 , one finds that every polynomial is a continuous function and that

$h(x) = \frac{f(x)}{g(x)}$ is continuous for $g(x)\neq 0$ , where $f, g\in \mathbb{R}[x]$ .

Verify the claim in Remark 5.59 .

More advanced (transcendental) functions like $\sin(x)$ and $e^x$ also turn out to be continuous. We will return to this in the next chapter, where differentiable functions are defined.

Show from scratch (without using Remark 5.59 ) that

$g(x) = \dfrac{a(x)}{b(x)}$

is a continuous function $g: V\rightarrow \mathbb{R}$ , where $a(x) = x^2 - 3 x + 2$ and $b(x) = x^2 - 4 x + 3$ and

$V = \mathbb{R}\setminus\{1, 3\}.$

Use Proposition 5.42 and Proposition 5.51 to show that

$\{x\in \mathbb{R} \mid a(x) \leq 17\}$

is a closed subset of $\mathbb{R}$ .

Hint

Write

$\{x\in \mathbb{R} \mid a(x) \leq 17\} = a^{-1}(S),$ where $S\subseteq \mathbb{R}$ is a suitable (closed) interval.

Does

$\lim_{x\to 3} g(x)$ exist? What about

$\lim_{x\to 1} g(x)?$

5.8 Important and special results for continuous functions

Below we quote a famous and very intuitive result from 1817 due to Bolzano. This result is also known as the intermediate value theorem.

Let $f: [a, b]\rightarrow \mathbb{R}$ be a continuous function, where $a < b$ . If $f(a) < 0$ and $f(b) > 0$ , then there exists $x_0$ with $a < x_0 < b$ , such that $f(x_0) = 0$ .

Polynomials are continuous functions. Bolzano's result fits perfectly in the proof of the result below. This result is wrong for polynomials in $\mathbb{Q}[x]$ as witnessed by $f(x) = x^3-2$ , which does not have a rational root.

Use the methods of Example 1.38 to show that there is no $\xi\in \mathbb{Q}$ with $f(\xi) = 0$ , where $f(x) = x^3-2$ .

Let

$f(x) = a_n x^n + \cdots + a_1 x + a_0\in \mathbb{R}[x]$ be a polynomial of odd degree, i.e. $n$ is odd and $a_n\neq 0$ . Then $f$ has a root, i.e. there exists $x_0\in\mathbb{R}$ , such that $f(x_0) = 0$ .

We will assume that $a_n > 0$ (if not, just multiply $f$ by $-1$ ). Consider $f(x)$ written as

$f(x) = x^n \left(a_n + \frac{a_{n-1}}{x} + \cdots + \frac{a_1}{x^{n-1}} + \frac{a_0}{x^n}\right).$ By choosing $c$ negative with $\left\vert c \right\vert$ extremely big, we have $f(c) < 0$ , since $c^n$ is negative and

$a_n + \frac{a_{n-1}}{c} + \cdots + \frac{a_1}{c^{n-1}} + \frac{a_0}{c^n} > 0$ as $a_n$ is positive. Notice here that the terms

$\frac{a_{n-1}}{c} + \cdots + \frac{a_1}{c^{n-1}} + \frac{a_0}{c^n}$ are extremely small, when $\left\vert c \right\vert$ is extremely big.

Similarly by choosing $d$ positive and tremendously big, we have $f(d) > 0$ . By Theorem 5.63 , there exists $x_0$ with $c < x_0 < d$ with $f(x_0) = 0$ .

We end this section with a result that might be coined the mathematical cornerstone of optimization (also due to Bolzano, at least for $n=1$ ). The result below is called the extreme value theorem.

Let $C$ be a compact subset of $\mathbb{R}^n$ and $f: C\rightarrow \mathbb{R}$ a continuous function. Then there exists $v_{\min}, v_{\max}\in C$ , such that

$f(v_{\min}) \leq f(v)\qquad\text{and}\qquad f(v)\leq f(v_{\max})$ for every $v\in C$ .

This is a rather stunning result! You are guaranteed solutions to optimization problems of the type

$\begin{aligned} &\text{Minimize} &f(v)&\\ &\text{with constraint}\\ &&v\in C, \end{aligned}$

where $C$ is a compact subset and $f: C\rightarrow \mathbb{R}$ a continuous function. Finding the optimal solutions in this setting is another story. It can be extremely hard. For the rest of these notes we will actually dive into methods for computing optimal solutions of optimization problems such as the one above.

Give two examples, where Theorem 5.66 fails for $n=1$ if we relax the conditions on $C$ . One, where $C$ is open and another one where $C$ is not bounded.