7Several variables
7.1 Introduction

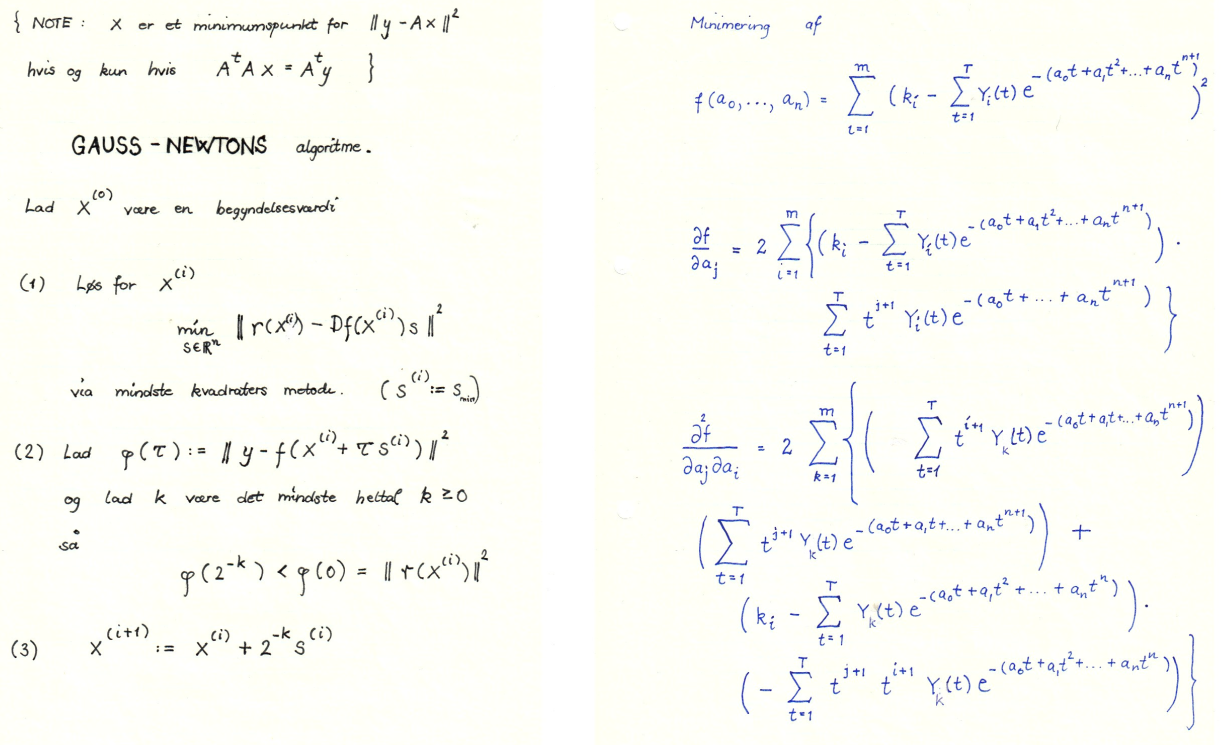

Illustrate the gradient descent method for . Pay attention to
the learning rate . How big is allowed to be, when
is required and ?
This is a hands-on exercise: carry out the gradient descent method
numerically for the function
to solve the minimization problem
starting with .
Hint
Is a convex function?
Explain how the
Newton-Raphson method
This is an iterative method for approximating a zero for a differentiable function . It works by guessing and then iterating to get a sequence approximating a zero ().
may be used to solve the minimization problem and
compute the minimum also using this method.
Helpful code
It is not clear how to choose the step size here. Proceed by letting be the
smallest natural number, such that
Stop the process, when .
Helpful code
7.2 Vector functions
Look back at Exercise
1.115
. Write down precisely the
vector function occuring there.
The function is rotating
a vector degrees counter clockwise. What are
and in
Hint
Try rotating some specific vectors like degrees.
Do you see a pattern?
7.3 Differentiability
Let be a
function with an open subset. Then is
differentiable at if there exists
The function is called
differentiable if it is differentiable at every .
- an matrix ,
- an open subset with , such that for every ,
- a function continuous at with ,
7.3.1 Partial derivatives
Let be a function, where is an open subset
of . Fix a point and let
for . If is differentiable at according to Definition
7.3
, then
we say that the partial derivative
of with respect to exists at and use the notation
The partial derivative with respect to a specific variable is computed by
letting all the other variables appear as constants.
Consider the function given by
Then
where . This example illustrates that
can be computed just like in the
one variable case, when the other variables () are treated
as constants. Notice that
Use the Sage window above to verify the computation of the partial
derivative in Example
7.9
.
Let be a function with an
open subset. If is differentiable at , then the
partial derivatives
exist for and and the matrix
in Definition
7.5
is
The -th column in is . Putting for
in Definition
7.5
gives
The -th coordinate of this identity of -dimensional vectors
can be written
where
and
(7.6)
shows that .
Compute the matrix derivative of the vector function in Exercise
7.4
.
Let be a function with an
open subset. If the partial derivatives for exist at every with
continuous (for and ), then
is differentiable. If the second order partial
derivatives exist for a function
and are continuous functions,
then
for .
Verify (by hand!) the symmetry of the second order partial derivatives for the function
in Example
7.9
i.e., show that
Verify that given by
is a differentiable function by computing
and applying Theorem
7.13
. Check also that
7.4 Newton-Raphson in several variables!
Verify the claim in
(7.10)
by applying
(7.8)
to
Carry out sufficiently many iterations starting with the vector in
(7.10)
to see the iteration stabilize. You should do this
using a computer, for example by modifying the Sage code in the last half of Example
7.18
.
7.5 Local extrema in several variables
Let be a function, where is
an open subset. Suppose that the partial derivatives exist at
. Then is called a critical
point for if .
Consider the function given by
corresponding to finding critical points for the function
You can left click and hold the graph computed below (after it has rendered) and rotate
the surface to get a feeling for what
(7.11)
looks like. Zooming in is also possible.
Here
In the Sage code below, Newton's method is started at and iterated four times.
Let be a differentiable function, where
is an open subset. Suppose that and
for . Then
for small.
By the differentiability of ,
where is a function satisfying
for . For
with we have
When tends to zero from the right, it follows that for small .
Let us briefly pause and see Lemma
7.19
in action. Consider the function
given by
and with
.
In this case and
. Therefore we may find a small , such that .
How do we choose optimally? If is too big we fail and land up in a worse point than .
Here
This is a quadratic polynomial, which is minimal for
. Therefor the minimal value reached in the direction of is .
The process now continues replacing by .
Let be a differentiable function, where
is an open subset. If is a local
extremum, then is a critical point for .
Suppose that . If is a local minimum,
then we may use in
Lemma
7.19
to deduce that for small. This contradicts the local minimality
of . If is a local maximum we can apply
Lemma
7.19
with and
to reach a similar contradiction. Therefore and
is a critical point for .
Compute the critical points of
Is a local maximum or a local minimum for ?
Hint
Look at
and and (along with Theorem
6.47
).
We will prove later that a differentiable function is
strictly convex if the socalled Hessian matrix given by
is positive definite for every . This is a multivariable generalization of
the fact that is strictly convex if for every
.
Now let
3D graph
You can left click the surface computed below after it has rendered and rotate
or zoom in.
- Show that is strictly convex.
-
Compute the critical point(s) of .HintThis is a numerical computation! Modify the relevant Sage window for Newton's method in the previous chapter to do it.
-
For a differentiable convex function we have in general that
for every . This is a multivariable generalization of Theorem
6.58
.Explain how one can use (7.13) to find a global minimum for the function in (7.12) . Is this minimum unique? Is for every ?
7.6 The chain rule
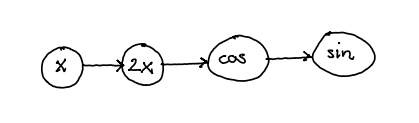
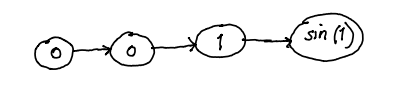
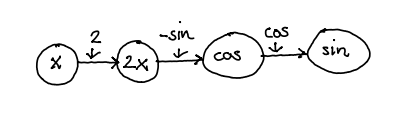
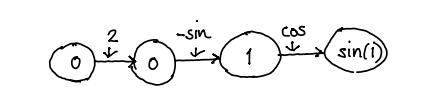
Let and with
, open subsets and
. If is differentiable at and is
differentiable at , then is differentiable
at with
7.6.1 Matrix multiplication graphically
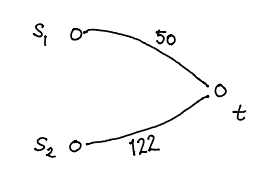
The matrix
is represented below as a graph
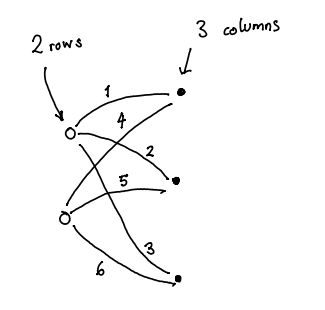 Similarly the matrix
is represented as
Similarly the matrix
is represented as
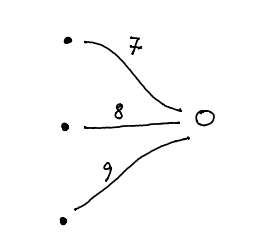 You know that the matrix product is a matrix. Let us line and up
graphically:
You know that the matrix product is a matrix. Let us line and up
graphically:
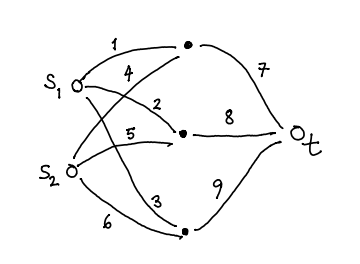 There are three paths from to and three paths from to . Here are the three paths from
to :
There are three paths from to and three paths from to . Here are the three paths from
to :
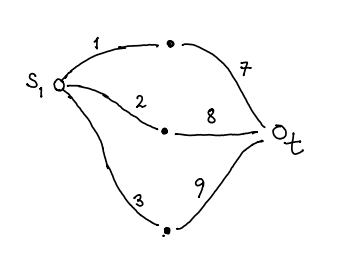 Finally, the matrix product is represented by the graph
Finally, the matrix product is represented by the graph
 The number on the edge from to is gotten by adding the products of the weights on
each of the three paths from to i.e., . This is the graphical interpretation of matrix multiplication!
The number on the edge from to is gotten by adding the products of the weights on
each of the three paths from to i.e., . This is the graphical interpretation of matrix multiplication!





7.6.2 Unpacking the chain rule
The function given by
may be evaluated using the computational graph
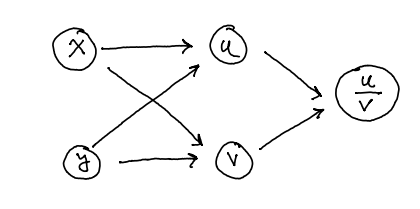 where is the function and is the function .
Similar to the one variable case discussed in the beginning of section
7.6
,
we label each edge, but now by the partial derivative of the function in its ending node
with respect to the variable in its beginning node:
where is the function and is the function .
Similar to the one variable case discussed in the beginning of section
7.6
,
we label each edge, but now by the partial derivative of the function in its ending node
with respect to the variable in its beginning node:
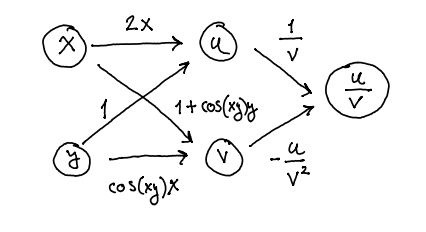 From the graphical interpretation of the matrix product and the chain rule you follow
the two paths from the input node to the output node and conclude that
From the graphical interpretation of the matrix product and the chain rule you follow
the two paths from the input node to the output node and conclude that


Construct a computational graph for
and detail the computation of the gradient in this context.
Compute the
gradient of at using pytorch.
Consider and
given by
Compute using the chain rule and check the result
with an explicit computation of the derivative of .
We wish to show that the function given by
is convex. This means that we need to prove that
for every and every with .
This can be accomplished from the one variable case in the following way. Define
and show that is convex by using the chain rule to show that . Show
how the convexity of follows from this by using that
7.7 Logistic regression
Prove that
and
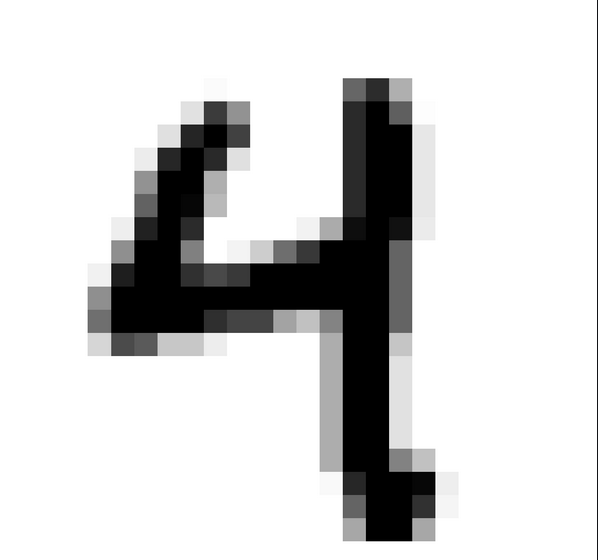
7.7.1 Estimating the parameters
Suppose that the event is assumed to be dependent on only one observation i.e., above.
For example, could be the event of not showing up on a Monday paired with the amount of sleep
in the weekend.
Here
and
I remember exactly where I was when first hearing about
the
Challenger
See byuistats.github.io for more details on this example
disaster in 1986.
This dreadful event was caused by failure of a socalled O-ring. The
O-rings had been tested before the launch for failure (=1 below) at different
temperatures (in F) resulting in the (partial) table below.
At the morning of the launch the outside temperature was
(uncharacteristically low for Florida) degrees Fahrenheit. We
wish to use logistic regression to compute the probability that the
O-ring fails.
Below we have sketched how the logistic regression is carried out using the python library SciKit-Learn.
The option solver='lbfgs' chooses an algorithm for maximizing .
Press the
Compute button and see the probability of failure during the launch.
💬
Explain the function LogicsticRegression in sklearn. In particular, what do the
parameters in
model = LogisticRegression(C=25, solver='lbfgs')
model.fit(X,y)
mean?
7.8 3Blue1Brown
7.8.1 Introduction to neural networks
7.8.2 Gradient descent
7.8.3 Backpropagation and training
7.8.4 The chain rule in action
Watch the video above before solving this exercise.
Consider the simple neural network
 where
and is the sigmoid function. This neural network has input
and output . Let be a function of the output . For fixed
, we consider as a function of via
Backpropagation for training neural networks is using the
chain rule for computing the gradient
Explain how to do this.
where
and is the sigmoid function. This neural network has input
and output . Let be a function of the output . For fixed
, we consider as a function of via
Backpropagation for training neural networks is using the
chain rule for computing the gradient
Explain how to do this.
7.9 Lagrange multipliers
Suppose that is a local maximum/minimum for
(7.18)
. Then there exists
, such that is a critical point for .
Consider the minimization problem
First of all, why does this problem have a solution at all? We write
the non-linear equations
up coming from the critical points of the Langrange function. Now we know that
these can be solved and that amongst our solutions there is a minimum!
Computing the distance from the line to the point gives rise to the
minimization problem
Solve this minimization problem using Theorem
7.37
.
Use Theorem
7.37
to
maximize subject to .
Hint
Consider the subset
. Why is a closed subset?
Why is bounded?
Hint
How does this relate to Theorem
5.66
?
Does the optimization
problem have a geometric interpretation?
Hint
Here you end up with the system
of linear equations in and , where you
regard as a constant. Use Gaussian
elimination to solve this system in order to
derive a (nice) quadratic equation in coming from
where you assume that . Handle the case separately.
To prove that is bounded you can keep fixed in
and solve for . A last resort is using the plot in Sage in the Hint button below, but that
does not give any real insight unless you explain how Sage makes the plot from
the equation
(7.21)
.
A rectangular box has side lengths , and . What is its
maximal volume when we assume that lies on the plane
for .
A company is planning to produce a box with volume
. For design reasons it needs different
materials for the sides, top and bottom. The cost of the materials
per square meter is dollar for the sides, dollars for the
bottom and the top. Find the measurements of the box minimizing the
production costs.
Hint
Let and be the measurements. Use to
rewrite the Lagrange equations so that and are expressed in terms
of .
7.10 Optimization using the interior and boundary of a subset
Consider an optimization problem
where is a subset, a
differentiable function and an optimal solution to
(7.22)
. If , then is a critical point of .
Consider the minimization problem
from Example
7.38
. Let us modify it to
where
We are now minimizing not only over the unit circle, but
the whole unit disk. Here
Proposition
7.44
guides us first to look for
optimal points in . Here we use Proposition
7.21
to
show that there can be no optimal points in , because
the gradient of the function is
Therefore the boundary needs to be analyzed and the usual technique
(as was implicit in Lagrange multipliers) is to find
a parametrization for the points satisfying
. There are two of those (one for the upper unit circle and one for the lower unit circle):
where .
This means that the optimization problem for the boundary turns into the two
simpler optimization problems of minimizing
subject to . These can as one variable optimization problems be solved the usual way.
Solve the two optimization problems
where . But first give a
reason as to why they both are solvable.
Hint
First find and . Then try with Proposition
7.44
supposing that a maximal point really is to be found in and not
on .
Solve the two optimization problems
where . But first give a
reason as to why they both are solvable.
Solve the two optimization problems
where is the triangle with vertices in and . But first give a
reason as to why they both are solvable.
Use Proposition
7.44
to give all the minute details in applying
Theorem
7.37
to solve Exercise
7.42
.
First rewrite to the problem, where you minimize subject to by using .
Then explain why this problem may be solved by restricting with upper and lower bounds on and . The minimum () is attained in a critical point and not on the
boundary. For one may optimize over the compact subset
and analyze what happens when .